Простые инструменты крнтроля качества. Гистограммы

Гистограмма является графическим представле­нием изменчивости имеющихся данных; она способ­ствует выявлению структуры и характера изменения данных, которые не заметны при их табличном пред­ставлении. Гистограмма представляет собой столбчатый график, построенный по полученным за определен­ный период (неделю, месяц и т. д.) данным, которые разбиваются на интервалы. Число наблюдений, попав­ших в каждый из интервалов (частота), выражается высотой столбика.

Для надежной гистограммы требуется не менее 40 наблюдаемых значений.

Алгоритм построения гистограммы.

1. Вычисление размаха выборки R (разности между максимальным и минимальным наблюдаемыми зна­чениями выборки).

2. Определение размера интервалов путем деления размаха выборки на равные части (от 6 до 20). Ре­комендуемое число интервалов гистограммы пред­ставлено в табл. 5.

Таблица 5. Рекомендуемое число интервалов гистограммы.

Количество наблюдаемых значений в выборке	Число интервалов
40-50
51-100
101-200
201-500
501-1000
Более 1000	11-20

3. Подготовка бланка регистрации распределения зна­чений для занесения интервала, отметки попаданий значений в интервал и итогового числа частот.

4. Оформление гистограммы.

По изображенному на гистограмме распределению определяют, в удовлетворительном ли состоянии нахо­дится наблюдаемая партия изделий и технологический процесс ее изготовления. Для этого, исходя из установ­ленных допусков, выясняют следующие вопросы:

• Какова форма распределения?

• Каково соотношение широты распределения и ши­роты допуска?

• Каково расположение центра распределения по от­ношению к центру поля допуска?

Ниже приведены различные сочетания плотности расцределения наблюдаемых значений с пределами до­пуска (НП — нижний предел, ВП — верхний предел).

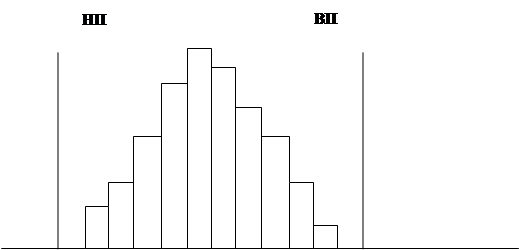Распределение симметричное. Широта распределе­ния составляет примерно 80% широты допуска. Партия находится в удовлетворительном состоянии. Вмеша­тельство в производственный процесс не требуется.

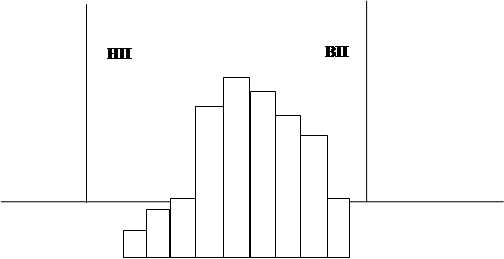
Распределение смещено вправо. Возможно, что в ос­тальной части партии существуют дефектные изделия, выходящие за верхний предел допуска. Необходима проверка измерительной техники на наличие система­тической ошибки.

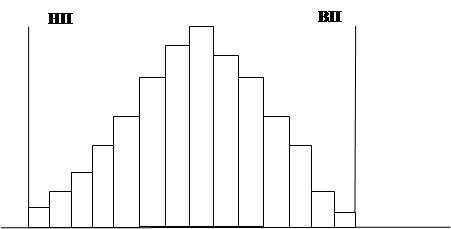Распределение симметричное. Широта распределе­ния совпадает с широтой допуска. При продолжении производства возможно появление дефектных изделий со стороны любого из пределов допуска. С целью суже­ния широты распределения нужно, например, обследо­вать условия производства изделий.

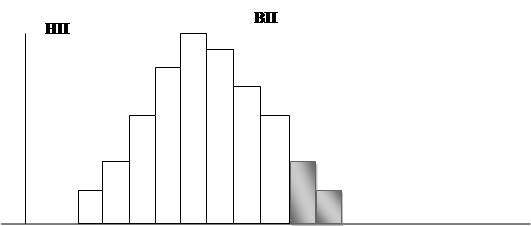Распределение симметричное, но со смещенным центром. Широта распределения и широта допуска оди­наковы. Необходимо смещение центра распределения к центру допуска.

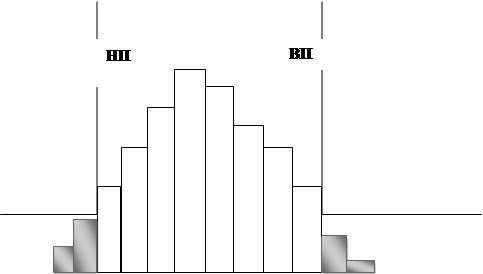
Центры распределения и поля допуска совпадают, но широта распределения превышает широту поля до­пуска. Для ликвидации дефектов в изделиях необходи­мы срочные меры.

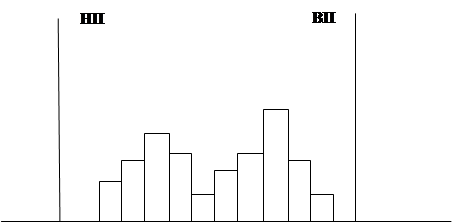Двухпиковое распределение. Нужны два дополни­тельных обследования (по каждому «пику» отдельно).

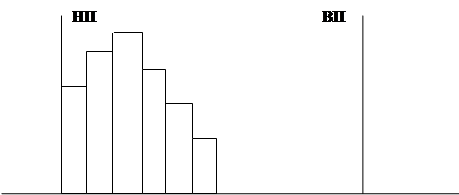
Левая сторона распределения «оборвана». Центр распределения смещен. Возможно, допущено искажение данных или требуется исправление какого-либо пара­метра. Гистограмма дает возможность общего диагностиро­вания состояния качества партии изделий по внешней форме распределения, однако она не содержит количе­ственной информации, например, о симметричности правой и левой сторон распределения или о его широ­те. Для получения таких данных необходимо рассчитать среднее арифметическое и дисперсию распределения.

Дата добавления: 2014-01-15