
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Обыкновенных дифференциальных уравнений
|
|
|
|
Тема1. ПОНЯТИЕ О КРАЕВОЙ ЗАДАЧЕ ДЛЯ
ЗАДАЧА ШТУРМА-ЛИУВИЛЛЯ
 Понятие о краевой задаче.
Понятие о краевой задаче.
Для определения постоянных, входящих в общее решение дифференциального уравнения, необходимо задавать дополнительные условия.
Задача Коши:
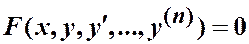 , (1.1)
, (1.1)
начальные условия для определения постоянных
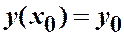 ,
, 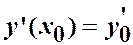 , …,
, …, 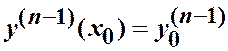 .
.
В задаче Коши начальные условия задаются в одной точке 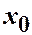 .
.
В приложениях часто возникают задачи, когда дополнительные условия задаются в двух точках, обычно на концах того промежутка, на котором производится интегрирование уравнения. Такого рода условия называются граничными или краевыми условиями. Их число должно равняться порядку уравнения.
Пример 1. (Задача о попадании материальной точки массы 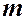 под действием внешней силы
под действием внешней силы 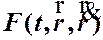 в заданную точку).
в заданную точку).
Найти закон движения материальной точки, если в начальный момент 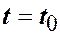 точка находилась в положении
точка находилась в положении 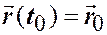 , а в момент
, а в момент  должна попасть в точку
должна попасть в точку 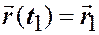 .
.
Задача сводится к интегрированию уравнения
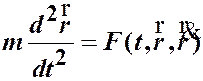 (1.2)
(1.2)
с краевыми условиями 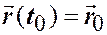 ,
, 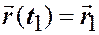 .
.
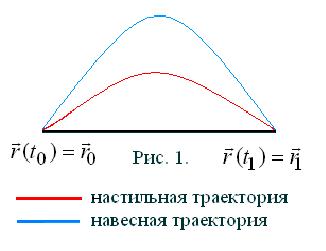
Эта задача имеет неоднозначное решение (рис. 1).
|
Если удаётся найти общее решение дифференциального уравнения краевой задачи, то для получения частного решения задачи надо определить произвольные постоянные из граничных условий. При этом далеко не всегда существует действительное решение, а если существует, то оно не обязательно единственное.

 Общая схема решения краевой задачи.
Общая схема решения краевой задачи.
Пусть имеется линейное однородное дифференциальное уравнение второго порядка с однородными краевыми условиями:
 ,
, 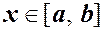 (1.3)
(1.3)
где 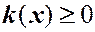 ,
, 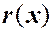 и
и 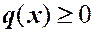 - функции, непрерывные на конечном отрезке
- функции, непрерывные на конечном отрезке 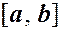 ,
, 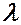 числовой параметр.
числовой параметр.
Пусть на концах отрезка заданы краевые условия
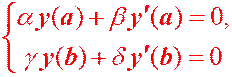 (1.4)
(1.4)
Пусть 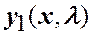 ,
, 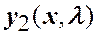 линейно независимые решения уравнения (1.3).
линейно независимые решения уравнения (1.3).
Общее решение уравнения (1.3) имеет вид
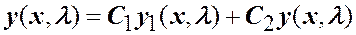 (1.5)
(1.5)
Для простоты, рассмотрим частный случай краевых условий (1.4):
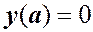 ,
,  (1.6)
(1.6)
Для определения постоянных 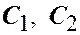 из краевых условий получаем однородную линейную систему алгебраических уравнений:
из краевых условий получаем однородную линейную систему алгебраических уравнений:
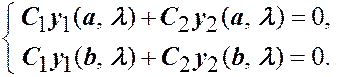 (1.7)
(1.7)
Если значение параметра 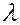 таково, что система (1.7) имеет только нулевое решение
таково, что система (1.7) имеет только нулевое решение 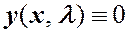 , то решение называется тривиальным.
, то решение называется тривиальным.
Если же 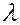 удовлетворяет уравнению
удовлетворяет уравнению
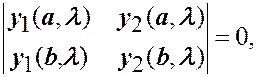 (1.8)
(1.8)
то система (1.9), а, следовательно, и задача (1.3), (1.6) имеет решение, отличное от нулевого, определенное с точностью до постоянного множителя. Других решений при заданном значении 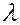 задача не имеет, так как все решения, имеющие корень
задача не имеет, так как все решения, имеющие корень  , линейно зависимы.
, линейно зависимы.
Аналогично решается общая задача с краевыми условиями (1.4).
Задача нахождения значений параметра 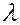 , при которых уравнение
, при которых уравнение
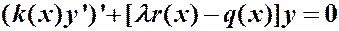 ,
, 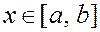
с краевыми условиями
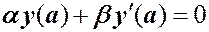 ,
, 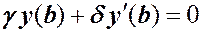
имеет ненулевое решение, называется задачей Штурма – Лиувилля.
Значения параметра 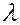 , при которых данная задача имеет решение
, при которых данная задача имеет решение 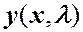 , отличное от тривиального решения, называются собственными значениями задачи.
, отличное от тривиального решения, называются собственными значениями задачи.
Решения 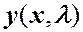 , отвечающие данному собственному значению
, отвечающие данному собственному значению 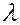 , называются собственными функциями задачи.
, называются собственными функциями задачи.
Пример 2. Рассмотрим задачу 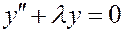 ,
,  ,
,
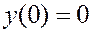 ,
, 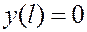 .
.
1. Пусть 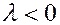 . Обозначим
. Обозначим  . Тогда общее решение уравнения будет
. Тогда общее решение уравнения будет  .
.
Из краевых условий получаем систему для определения постоянных 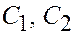 :
:
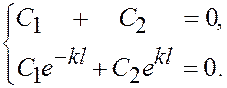
Приравнивая определитель системы к нулю,
получаем уравнение:
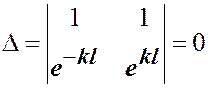 ,
, 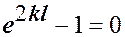 ,
, 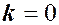 ,
,
что противоречит принятому условию 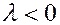 .
.
2. Пусть 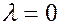 . Тогда общее решение уравнения имеет вид
. Тогда общее решение уравнения имеет вид 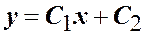 .
.
Из краевых условий получаем 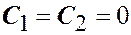 ,
, 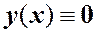 .
.
3. Рассмотрим положительные значения 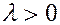 . Общее решение уравнения:
. Общее решение уравнения:
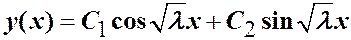 .
.
Из краевых условий получаем систему:
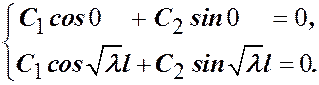
Из первого уравнения следует 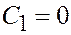 . Из второго уравнения получаем
. Из второго уравнения получаем  . Постоянная
. Постоянная 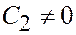 , так как иначе получаем
, так как иначе получаем 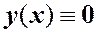 . Следовательно, для определения собственных значений
. Следовательно, для определения собственных значений 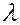 получаем уравнение
получаем уравнение
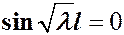 ,
, 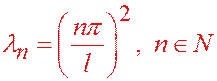 .
.
Соответствующие собственные функции: 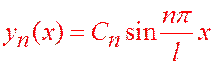 , где
, где 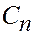 - произвольные постоянные.
- произвольные постоянные.
Замечание. Если в уравнении (1.3) функция  обращается в нуль на одном из концов отрезка
обращается в нуль на одном из концов отрезка 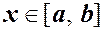 , например
, например 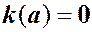 , то соответствующее этому концу краевое условие в (1.4) заменяется условием ограниченности решения
, то соответствующее этому концу краевое условие в (1.4) заменяется условием ограниченности решения 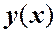 на этом конце.
на этом конце.
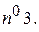 Общие свойства собственных функций и собственных значений задачи Штурма – Лиувилля.
Общие свойства собственных функций и собственных значений задачи Штурма – Лиувилля.
1. Существует бесчисленное множество собственных значений
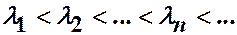 , которым соответствуют собственные функции
, которым соответствуют собственные функции 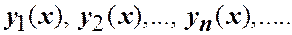
2. При 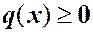 все собственные значения неотрицательные
все собственные значения неотрицательные 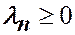 .
.
3. Собственные функции 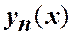 и
и 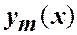 , соответствующие разным собственным значениям
, соответствующие разным собственным значениям 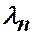 и
и 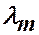 , ортогональны между собой с весом
, ортогональны между собой с весом 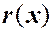 :
:
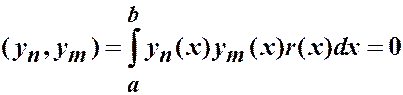 ,
, 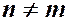 .
.
4. Справедлива теорема разложения В. А. Стеклова: функция 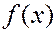 , дважды непрерывно дифференцируемая и удовлетворяющая краевым условиям (1.4), разлагается в абсолютно и равномерно сходящийся ряд по собственным функциям
, дважды непрерывно дифференцируемая и удовлетворяющая краевым условиям (1.4), разлагается в абсолютно и равномерно сходящийся ряд по собственным функциям 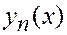
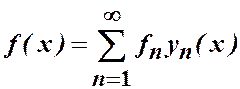 ,
,  , (1.9)
, (1.9)
если 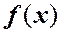 :
:
· имеет при 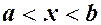 непрерывную первую и кусочно-непрерывную вторую производные;
непрерывную первую и кусочно-непрерывную вторую производные;
· удовлетворяет граничным условиям задачи;
· при этом если 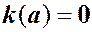 , то
, то 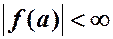 при
при 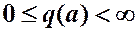 и
и 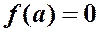 при
при 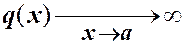 .
.
 Неоднородная краевая задача.
Неоднородная краевая задача.
Задача может быть неоднородной вследствие дифференциального уравнения или вследствие краевых условий. Рассмотрим неоднородное уравнение с однородными краевыми условиями
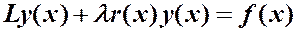 (1.10)
(1.10)
в области  , где
, где  ,
,
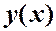 подчиняется однородным граничным условиям (1.4),
подчиняется однородным граничным условиям (1.4), 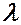 - заданная постоянная.
- заданная постоянная.
Решаем задачу Штурма – Лиувилля для однородной задачи:
 ,
,
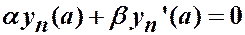 ,
, 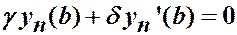 ,
,
и находим собственные значения и собственные функции дифференциального оператора 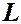 .
.
Разложим 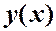 и
и  по собственным функциям оператора
по собственным функциям оператора 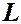 :
:
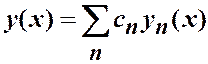 ,
,  (1.11)
(1.11)
и подставим в уравнение (1.10):
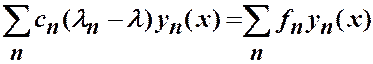 .
.
Так как собственные функции 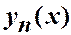 линейно независимы, то
линейно независимы, то
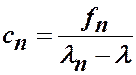 , или
, или 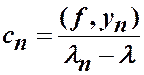 ,
,
где 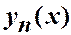 рассматриваются как нормированные функции. Поэтому
рассматриваются как нормированные функции. Поэтому
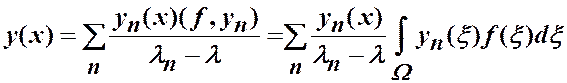 . (1.12)
. (1.12)
Это выражение можно записать по-другому
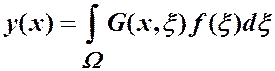 , (1.13)
, (1.13)
где 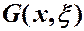 называется функцией Грина или фундаментальным решением краевой задачи:
называется функцией Грина или фундаментальным решением краевой задачи:
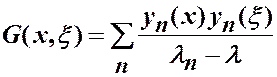 . (1.14)
. (1.14)
Вид функции Грина зависит от дифференциального оператора 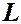 , области
, области  и краевых условий.
и краевых условий.
Таким образом, знание функции Грина 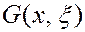 позволяет записать решение неоднородного уравнения с правой частью
позволяет записать решение неоднородного уравнения с правой частью 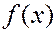 .
.
Нахождение функции Грина поясним на примере.
Пример 3. Найти функцию Грина краевой задачи: 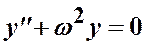 ,
, 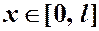 ,
,
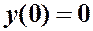 ,
, 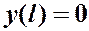 .
.
Собственные значения задачи найдены в примере 2 и равны 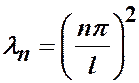 , нормированные собственные функции
, нормированные собственные функции 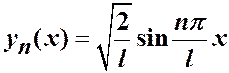 .
.
Следовательно, функция Грина равна:
 .
.
Задание 1.
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 966; Нарушение авторских прав?; Мы поможем в написании вашей работы!