Границя послідовності

ЛЕКЦІЯ 7: ЕЛЕМЕНТИ ТЕОРІЇ ГРАНИЦЬ

Якщо кожному натуральному числу за певним правилом ставиться у відповідність деяке дійсне число 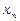, то множину чисел 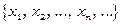називають послідовністю (числовою послідовністю) і позначають символом 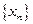. Числа є членами (елементами) послідовності, 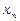- загальним членом послідовності.

Число називається границею послідовності 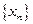, якщо для будь-якого числа можна знайти такий номер 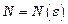, що при всіх 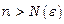виконується нерівність

. (5.1)

При цьому пишуть 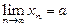або .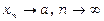

Довільний інтервал вигляду , де , називається околом точки . Якщо число є границею послідовності 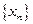, то для будь-якого можна знайти такий номер 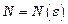, що при 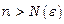усі члени послідовності потраплять в окіл точки .

Якщо послідовність має скінчену границю, то вона називається збіжною. Якщо послідовність не збігається, то кажуть, що вона є розбіжною.

Збіжну до нуля послідовність називають нескінченно малою.

Послідовність 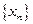називається нескінченно великою, якщо для будь-якого числа можна знайти такий номер 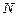, що при всіх 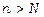виконуватиметься нерівність .

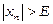Позначається це так: або .

Послідовність 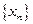називається обмеженою, якщо існує таке число 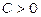, що при всіх виконується нерівність 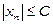. У противному разі послідовність називається необмеженою.

Послідовність 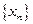називається обмеженою зверху (знизу), якщо існує таке число , що при всіх виконується нерівність .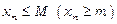

Послідовність 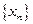називається зростаючою (спадною), якщо для будь-якого виконується нерівність .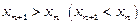

Послідовність 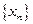називається неспадною (незростаючою), якщо для будь-якого виконується нерівність .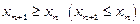

Неспадні і незростаючі послідовності називаються монотонними, а зростаючі й спадні – строго монотонними.

Нехай 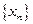– деяка числова послідовність, а 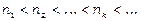– зростаюча послідовність натуральних чисел. Тоді послідовність 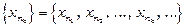називається підпослідовністю послідовності .

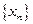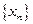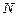Послідовність називається фундаментальною, якщо для будь-якого числа можна знайти такий номер , що при всіх виконуватиметься нерівність .

Сформулюємо основні властивості границь послідовностей.

1. Збіжна послідовність має тільки одну границю.

2. Будь-яка підпослідовність збіжної послідовності має ту саму границю, що й сама послідовність.

3. Послідовність 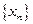збігається до тоді й тільки тоді, коли послідовність є нескінченно малою.

4. Якщо послідовність збіжна, то вона обмежена.

5. Алгебраїчна сума двох (або будь-якого скінченого числа) нескінченно малих є нескінченно малою.

6. Добуток двох (або будь-якого скінченого числа) нескінченно малих є нескінченно малою.

7. Добуток нескінченно малої на обмежену є нескінченно малою.

8. Для того, щоб послідовність була нескінченно малою, необхідно й достатньо, щоб 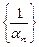була нескінченно великою.

9. Збіжна послідовність є обмеженою.

10. Нехай послідовност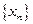і і 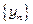збіжні, при цьому 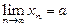, . Тоді збіжними є й послідовності 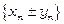, , 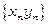(- стала), (остання при ), причому: ; ; ; .

11. Якщо 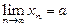, і 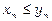для всіх , то .

12. Якщо 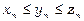для всіх і 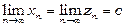, то й .

13. Обмежена зверху (знизу) неспадна (незростаюча) послідовність є збіжною.

14. З будь-якої обмеженої послідовності можна виділити збіжну підпослідовність.

15. Для того, щоб послідовність збігалась, необхідно й достатньо, щоб вона була фундаментальною.

Відомо, що важлива послідовність 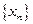із загальним членом є збіжною, причому

, (2)

де 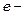константа Ейлера, .

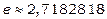При знаходженні границь послідовностей корисно пам’ятати, що

та .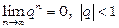

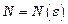Приклад 1. Знайти , і визначити номер такий, що при всіх .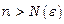

Легко бачити, що .

Скористаємося означенням границі послідовності. Для даної послідовності нерівність має вигляд

.

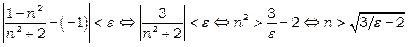Отже, 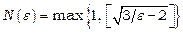, де квадратні дужки позначають цілу частину числа.

Приклад 2. Знайти границю послідовності .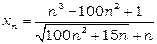

Чисельник і знаменник дробу є нескінченно великі послідовності, тому маємо невизначеність типу . Для розкриття цієї невизначеності винесемо в чисельнику і знаменнику дробу за дужки старші степені 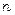. Дістанемо

.

Оскільки а чисельник дробу є нескінченно велика, то задана послідовність є нескінченно великою, тобто

.

Приклад 3. Знайти границю послідовності .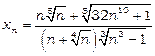

Маємо невизначеність типу , застосуємо той самий прийом, що й у попередньому прикладі.

.

Приклад 4. Знайти границю послідовності .

Оскільки послідовності і є нескінченно великі, тобто маємо невизначеність 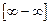, то для розкриття цієї невизначеності помножимо і поділимо загальний член послідовності на спряжений до нього вираз.

Приклад 5. Знайти границю послідовності .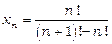

Маємо невизначеність . Оскільки 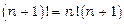, то

.

Приклад 6. Знайти границю послідовності

.

Загальний член заданої послідовності можна подати у вигляді , вирази у дужках є сумами членів спадних геометричних прогресій, тому

.

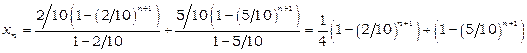Тоді .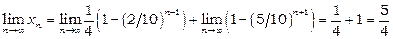

Приклад 7. Знайти границю послідовності

.

Оскільки послідовність прямує до 1, а послідовність нескінченно велика, то маємо невизначеність типу 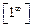, яка розкривається за допомогою границі (2). Представимо дріб у вигляді суми одиниці та нескінченно малої

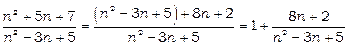
і скористаємося границею (2). Одержимо:

Дата добавления: 2014-01-11