Границя функції

Поняття границі функції є узагальненням поняття границі послідовності, оскільки границю послідовності можна розглядати як границю функції x_n = f (n) цілочисельного аргументу n.

Нехай задана функція f (x) і нехай a - гранична точка області визначення цієї функції D (f), тобто така точка, будь-який окіл якої містить точки множини D (f), відмінні від a. Точка a може належати множині D (f), а може й не належати їй.

Постійне число А називається границею функції f (x) при x®a, якщо для будь-якої послідовності { x_n } значень аргументу, що прямує до а, відповідні їм послідовності { f (x_n)} мають одну й ту ж границю А.

Це означення називають означенням границі функції за Гейне, або “ на мові послідовностей ”.

Постійне число А називається границею функції f (x) при x®a, якщо, задавши довільне як завгодно мале додатне число e, можна знайти таке d >0 (що залежить від e), що для всіх x, що лежать в d -околі числа а, тобто для x, що задовольняють нерівність 0<½ x-a ½< d, значення функції f (x) будуть лежати в e -околі числа А, тобто ê f (x)- A ê< e.

Це означення називають означенням границі функції за Коші, або “на мові e-d “.

Означення 1 і 2 рівносильні. Якщо функція f (x) при x®a має границю, рівну А, це записується у вигляді

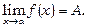(5.3)

У цьому випадку, якщо послідовність { f (x_n)} необмежено зростає (або спадає) при будь-якому способі наближення x до своєї границі а, то будемо говорити, що функція f (x) має нескінчену границю, і записувати це у вигляді:

().

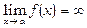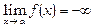Змінна величина (тобто послідовність або функція), що має своєю границею нуль, називається нескінченно малою величиною

.

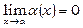Змінна величина, що має нескінчену границю, називається нескінченно великою величиною

.

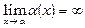Нехай 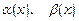- нескінченно малі при x®a. Якщ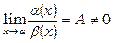о , то 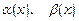називаються нескінченно малими одного порядку та пишуть 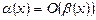при x®a.

Якщ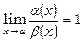о , то 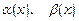називають еквівалентними та пишуть 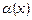~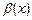при x®a.

Якщ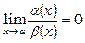о , то 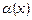називають нескінченно малою вищого порядку відносно 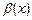та пишуть 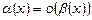при x®a.

Якщ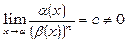о , то 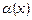називають нескінченно малою n-го порядку відносно .

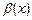Границя відношення двох нескінченно малих функцій не зміниться, якщо ці нескінченно малі замінити еквівалентними. Цей факт широко використовується при обчисленні границь.

Дата добавления: 2014-01-11