Важливі еквівалентні нескінченно малі

1) ~~~~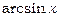~~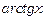 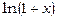х,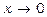

2) ~,

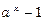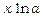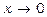
3) ~,

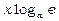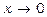
4) ~,

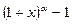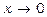
Для відшукання границь на практиці користуються такими теоремами.

Теорема 1. Якщо існують границі 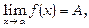, то

(5.4)

(5.5)

(B ¹0). (5.6)

Зауваження. Вирази вигляду 0/0, ¥/¥, 0×¥, ¥-¥ є невизначеними, наприклад, відношення двох нескінченно малих або нескінченно великих величин, і відшукання границь такого вигляду має назву “розкриття невизначеностей”.

Теорема 2. де a = const, (5.7)

тобто можна переходити до границі в основі степені при постійному показнику, зокрема,

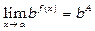, де b =const, 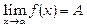; (5.8)

, де с =const. (5.9)

Теорема 3. 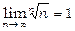, , 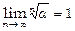a =const, a >0,

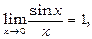(5.10)

, (5.11)

де e»2.718282... - основа натурального логарифма. Формули (5.10) та (5.11) мають назву першої та другої чудової границі.

Використовуються на практиці й наслідки формули (5.11):

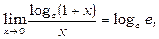(5.12)

(5.13)

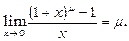(5.14)

зокрема,

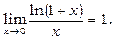
Якщо x®a і при цьому x>a, то пишуть x®a +0. Якщо, зокрема, a =0, то замість символу 0+0 пишуть +0. Аналогічно, якщо x®a і при цьому x<a, то пишуть x®a- 0. Числа 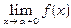і називаються відповідно границею справа та границею зліва функції f (x) в точці а. Для існування границі функції f (x) при x®a необхідно та достатньо, щоб .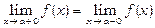

Функція f (x) називається неперервною в точці x ₀, якщо

(5.15)

Умову (15) можна переписати у вигляді:

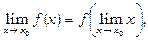
тобто можливий граничний перехід під знаком функції, якщо вона неперервна в даній точці.

Якщо рівність (15) порушується, то говорять, що при x=x _o функція f (x) має розрив. Розглянемо функцію y =1/ x. Областю визначення цієї функції є множина R, крім x =0. Точка x =0 є граничною точкою множини D (f), оскільки в будь-якому її околі, тобто в будь-якому відкритому інтервалі, що містить точку 0, є точки з D (f), але вона сама не належить цій множині. Значення f (x _o)= f (0) не визначене, тому в точці x _o=0 функція має розрив.

Функція f (x) називається неперервною справа в точці x _o, якщо

і неперервною зліва в точці x _o, якщо

Неперервність функції в точці x _o рівносильна її неперервності в цій точці одночасно і справа і зліва.

Для того, щоб функція була неперервна в точці x _o, наприклад, справа, необхідно, по-перше, щоб існувала скінчена границя 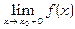, а по-друге, щоб ця границя була рівна f (x _o). Значить, якщо хоча б одна з цих двох умов не виконується, то функція буде мати розрив.

1. Якщо 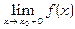,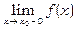існують і не дорівнюють f (x _o), то говорять, що функція f (x) в точці x _o має розрив першого роду, або стрибок.

2. Якщо 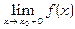=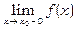і не дорівнюють f (x _o), то говорять, що функція f (x) в точці x _o має усувний розрив.

3. Якщо хоча б одне із значень 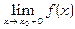, 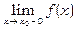дорівнює ¥ або не існує, то говорять, що в точці x _o функція має розрив другого роду.

Наприклад, функція y =ctg x при x ®+0 має границю, рівну +¥, значить, в точці x =0 вона має розрив другого роду. Функція y = E (x) (ціла частина від x) в точках з цілими абсцисами має розриви першого роду, або стрибки.

Функція, неперервна в кожній точці замкненого інтервалу (відрізку) [ a, b ], називається неперервною на [ a, b ]. Неперервна функція зображається суцільною кривою.

Дата добавления: 2014-01-11