Властивості функцій неперервних на відрізку

1. (І теорема Вейерштраса). Якщо функція неперервна на відрізку [ a, b ], то вона обмежена на цьому відрізку.

2. (ІІ теорема Вейерштраса). Якщо функція неперервна на відрізку [ a, b ], то вона досягає на цьому відрізку свого найменшого значення m та найбільшого значення М.

3. (Теорема Коші). Якщо функція неперервна на відрізку [ a, b ] і значення її на кінцях відрізку мають протилежні знаки, то всередині відрізку знайдеться точка 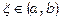така, що .

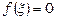До другої чудової границі приводять різноманітні задачі, пов’язані з неперервним ростом якої-небудь величини. До таких задач, наприклад, відносяться: зростання вкладу за законом складних відсотків, зростання населення країни, розпад радіоактивної речовини, розмноження бактерій та т.п.

Приклад 8. Довести, що .

Нехай 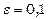. Тоді нерівність 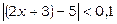буде виконуватись при 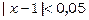. Аналогічно при 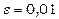та ж нерівність буде вірною при .

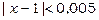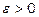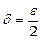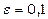
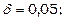Для будь-якого існує таке число (для для 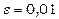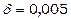і т.д.), що для всіх 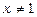і таких, що задовольняють умову 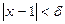, виконується нерівність 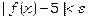, де 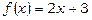; а це й означає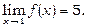

Приклад 9. Задана функція f (x)=2^{1/ x} . Довести, що не існує.

Скористаємось означенням 1 границі функції через послідовність. Візьмемо послідовність { x_n }, що збігається до 0, тобто 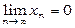. Покажемо, що величина для різних послідовностей поводить себе по-різному. Нехай x_n =1/ n. Очевидно, що 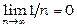, тоді . Виберемо тепер як x_n послідовність з загальним членом x_n = - 1/ n, яка теж збігається до нуля: 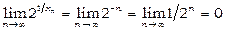. Тому не існує.

Приклад 10. Довести, що 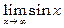не існує.

Нехай x ₁, x ₂,..., x_n,... - послідовність, для якої
. Як поводить себе послідовність { f (x_n)}={sin x_n } при різних x_n ®¥?

Якщо x_n=pn, то sin x_n =sin pn =0 при всіх n і 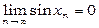. Якщо ж
x_n =2 pn + p /2, то sin x_n =sin(2 pn + p /2)=sin p /2=1 для всіх n і, значить, 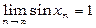. Таким чином, 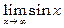не існує.

Приклад 11. Знайти .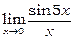

Маємо: . Позначимо t =5 x. При x ®0 маємо: t ®0. Застосовуючи формулу (8), отримаємо .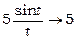

Приклад 12. Обчислити .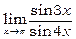

Позначимо y=p-x. Тоді при x®p, y ®0. Маємо:

sin 3 x =sin 3(p-y)=sin (3 p- 3 y)=sin 3 y.

sin 4 x =sin 4(p-y)=sin (4 p- 4 y)= - sin 4 y.

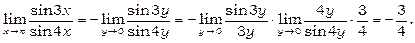
Приклад 13. Знайти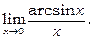

Позначимо arcsin x=t. Тоді x =sin t і при x ®0 t ®0.

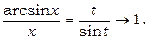
Приклад 14.

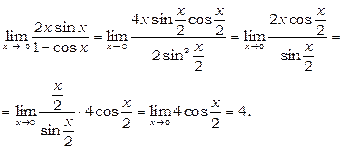
Приклад 15.

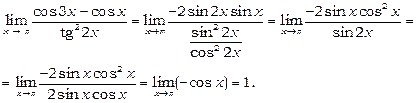
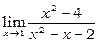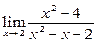Приклад 16. Знайти: 1); 2); 3).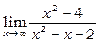

1. Застосовуючи теорему 1 про границю різниці та добутку, знаходимо границю знаменника: .

Границя знаменника не дорівнює нулю, тому, за теоремою 1 про границю частки, отримаємо: .

2. Тут чисельник і знаменник прямують до нуля, тобто має місце невизначеність виду 0/0. Теорему про границю частки безпосередньо не можна застосувати. Для “розкриття невизначеності” перетворимо дану функцію. Розділивши чисельник і знаменник на x- 2, отримаємо при x ¹2 рівність:

.

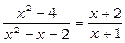Оскільки , то, за теоремою про границю частки, знайдемо

.

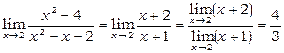3. Чисельник і знаменник при x ®¥ є нескінченно великими функціями. Тому теорема про границю частки безпосередньо не може застосовуватись. Розділимо чисельник і знаменник на x ² і до отриманої функції застосуємо теорему про границю частки:

.

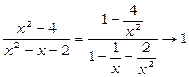Приклад 17.

Приклад 18. Знайти .

Тут чисельник і знаменник прямують до нуля: , , 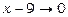тобто маємо невизначеність виду .

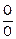Перетворимо дану функцію, помноживши чисельник і знаменник на неповний квадрат суми виразу , отримаємо

Приклад 19.

Приклад 20.

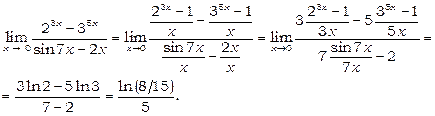
Приклад 21. Знайти .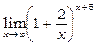

.

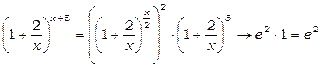Дата добавления: 2014-01-11