Тема 2: законы и уравнения идеальных газов

Резюме

Системы продаж часто не соответствуют продаваемому продукту, необходимо тщательно анализировать систему с целью обеспечения функциональной и экономической эффективности, а также безопасности бизнеса.

При проектировании необходимо обеспечить следующие требования:

1. Качество решения задач обслуживания (привлечение и удержание клиентов)

o Наличие необходимого вида обслуживания в нужное время

o Психологическое соответствие персонала решаемой задаче

o Функциональное соответствие персонала решаемой задаче

o Наличие у персонала необходимых ресурсов

2. Экономичность (умеренные затраты на содержание)

o Функции не должны дублироваться

o Простые функции должны выполняться низкооплачиваемыми сотрудниками

o Платить надо за решение важных для фирмы задач

3. Безопасность (предотвращение злоупотреблений)

o Ключевые функции должны находиться в руках лояльных сотрудников

o Ключевая информация и деятельность должна быть рассредоточена между сотрудниками

4. Бесконфликтность системы

o система не должна провоцировать межличностные конфликты в коллективе

o круг обязанностей и ответственности должен быть достаточно точно очерчен

Председатель Совета Директоров

Директор по продаже автомобилей

Директор по послепро- дажному обслужива-нию

Генеральный Директор

Исполнительный Директор

Финансовый Директор

Директор СТОА

Диспози- ция

Отдел продаж запасных частей

Административно-хозяйственный отдел.

Отдел рекламы и маркетинга

Бухгалтерия

Станция технического обслуживания

Отдел продаж легковых автомобилей

Отдел гарантийного обслуживания

Охрана

Отдел IT

Обменный пункт

Мойка автомобильная

Отдел продаж грузовых автомобилей

Отдел кадров

Парковка для клиентов

Главный инженер

Кассы

Парковка СТОА

Рисунок 1.

Типичная организация дилерской компании в автомобильном бизнесе (рис.1).В компании имеется отдел рекламы, отдел активных продаж, бухгалтерия и техническая служба.

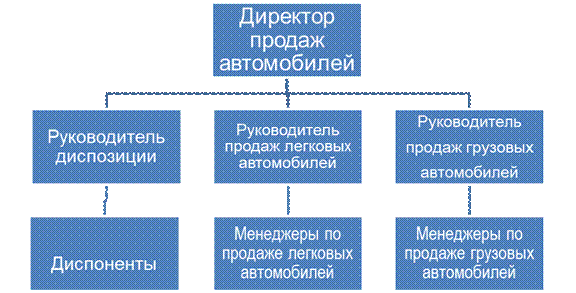
Рисунок 2.

Типичная организация направления продаж дилерской компании в автомобильном бизнесе (рис.2)

Директор по продажам автомобилей

Руководитель диспозиции

Руководитель продаж легковых автомобилей

Руководитель продаж грузовых автомобилей

Руководитель продаж б/у автомобилей

Руководитель группы технической поддержки

Диспоненты

Менеджеры по продаже легковых автомобилей

Менеджеры по продаже грузовых автомобилей

Менеджеры по закупкам и продажам

Специалисты технической поддержки

Рисунок 3

Типичная организация направления продаж дилерской компании в автомобильном бизнесе (рис.3) в фазе насыщения рынка.

Цели фирмы (в теории)

Максимизация темпов роста активов

Максимизация объёма прибыли

Максимизация объёма продаж

Цели фирмы (на практике)

Максимизация рыночной стоимости фирмы

Максимизация текущих финансовых результатов

Достижение заданного уровня рентабельности

Обеспечение стабильности

Максимизация рентабельности продаж

Максимизация рентабельности всех активов

Максимизация рентабельности собственного капитала

Цен

Рентабельности

Рыночной позиции

Рисунок 4

Лекция 3. Уравнения идеальных газов.

Уравнение Клапейрона. [ЗаконКлапейрона Бенуа Поля Эмиля (1799 – 1864), французского физика и инженера, установившего этот закон впервые в 1834 году, и дополненный Дмитрием Ивановичем Менделеевым (1834 – 1907),российским химиком, для одного моля идеального газа в 1874 году (уравнение состояния для идеального газа)] Законы Бойля – Мариотта, Гей-Люссака и Шарля устанавливают связь только между двумя из трех параметров идеального газа р, v и Т при условии, что значение третьего параметра остается неизменным. Установим, зависимость между тремя параметрами р, v и Т для всех случаев, когда газ находится в состоянии внутреннего равновесия. Возьмем цилиндр с подвижным поршнем (рис. 1).

Рис. 1. К выводу урав­нения Клапейрона

1, 2 – различные состояния идеального газа

В цилиндре (состояние 1) находится 1кг идеального газа с параметрами р ₁, v ₁ и Т ₁. При подведении или отнятии теплоты от газа и перемещении поршня можно перевести газ в другое состояние (2), при этом все его параметры изменятся и будут иметь значения: р ₂, v ₂ и Т ₂. Уравнение 6 (лекция 2) запишем для двух состояний газа:

и

Разделяя правые и левые части равенств, получим:

.

После перестановки средних членов пропорций полу­чим зависимость, которая называется объединенным за­коном Бойля – Мариотта и Гей-Люссака:

. (1)

Если в уравнении (1) постоянную величину обозна­чить через R, назвав ее удельной газовой постоянной, и отнести ее к 1 кг газа, то получим:

или. (2)

Уравнение (2) относится к состоянию идеального газа и применимо для равновесного его состояния. Оно связывает три основных параметра идеального газа. По известным значениям любых двух из них можно опре­делить значение третьего пара­метра. Впервые это уравнение предложил французский физик Клапейрон, именем которого оно названо (его называют также характеристическим). Клапейрон получил его на основании соче­тания законов Бойля – Мариот­та и Гей-Люссака. В уравнении Клапейрон не использовал зако­на Авогадро. Чтобы применить уравнение для какого-либо газа, необходимо изучить его свойства и определить величину R, кото­рая зависит от природы и коли­чества газа.

Для произвольной массы га­за т (кг) уравнение состояния получается путем умножения обоих членов уравнения (2) на величину т.

Так как V = vm, где V – полный объем газа, получим

, (3)

где р – абсолютное давление газа, Па;

V –объем газа, м³;

v – удельный объем, м³/кг;

т – масса газа, кг;

Т – абсолютная темпе­ратура К.

Газовая постоянная. Газовая постоянная R₁, вхо­дящая в уравнение (3) имеет размерность Дж/(кг∙К) и физически означает механическую работу, совершае­мую газом при расширении, если 1 кг его нагреть на 1 К при постоянном давлении. На основании уравнения (3) можно написать уравнение состояния для (μкг газа, т. е.

для киломоля газа

(4)

где V _μ=μ∙ v – объем киломоля;

μ– молекулярная масса;

R ₁– га­зовая постоянная, отнесенная, к 1 кг газа.

Из уравнения (4) определим газовую постоянную рассматриваемого газа:

. (5)

Учитывая, что объем 1 кмоля любого газа при нор­мальных условиях [ р = 101335 Па(760 мм рт. ст.) и температуре Т =273,16 К] занимает объем V _μ=22,4146 м³/моль, получим:

(5а)

или μ· R = 8314 = R _μ

где R _μ– постоянная Менделеева или универсальная газовая посто­янная, Дж/(К·моль).

Универсальная газовая постоянная, входящая в уравнение, состояния идеального газа численно равна работе расширения 1 моля идеального газа в изобариче­ском процессе при увеличении температуры газа на 1 К.

Уравнение Клапейрона – Менделеева. Исследуя свойства газов, великий русский ученый Дмитрий Иванович Менделеев нашел для всех идеальных газов уравнение состояния. Уравнение (4) можно записать в следующем виде:

или (6)

. (7)

Впервые оно было выведено Д. И. Менделеевым для 1 кмоля газа и называется уравнением Менделеева, или Клапейрона– Менделеева. Зная, что R _μ=8314 Дж/(кмоль·К), уравнение Менделеева запишем в следую­щем виде:

(8)

Умножив обе части уравнения (7) на п _μ– число киломолей газа, получим общее уравнение Менделеева, которое объединяет одновременно законы Бойля –Ма-риотта, Гей-Люссака и Авогадро:

или (9)

где V – объем п молей газа при абсолютных температуре Т и дав­лении р;

R _μ–постоянная Менделеева, или универсальная газовая постоянная.

Графически в системе координат р –V при p = const работа 1 кмоля газа показана на рис.2.

Рис. 2. Графическое изо­бражение работы газа

Для определе­ния величины удельной работы надо найти площадь, ог­раниченную координатами V ₁, 1, 2, V ₂. Воспользуемся формулой

L = p (V ₂ – V _l). (10)

Из уравнения состояния идеального газа имеем

и

Подставив эти данные в уравнение (10), получим

L = R (T ₂ – T ₁), откуда

Этим уравнением определяется физический смысл универсальной газовой постоянной как удельной работы.

Некоторые практические задачи. Законы и урав­нения идеальных газов имеют большое практическое значение. Основное уравне­ние газового состояния применяют при изучении работы двигателей внутреннего сгорания, различ­ных компрессоров и т. д. В этих приборах (машинах)одновре­менно в процессе работы меня­ются три параметра – давление, температура и объем. Широко применяются законы Бойля – Мариотта, Гей– Люссака и Шарля. Так, используя закон Бойля – Мариотта, можно вычислить объем остав­шегося в баллончике кислорода. Законы Бойля – Мари­отта, Гей –Люссака и Шарля часто используют при ре­шении задач безопасности на предприятиях, применяющих, перерабатывающих или производящих пожаро- и взры­воопасные газы (в том числе и на летательных аппаратах).

Задача 1. На складе хранятся баллоны с газом, давление в которых p ₁ = 200·10⁵ Па, температура окружающей среды t ₁ = 17°C. Определить, до какой температуры (в случае пожара) могут нагреть­ся баллоны, если они рассчитаны на предельное давление р ₂=350·10⁵ Па.

Решение. Используя уравнение Шарля (2.13), определим Т ₂;

К,

Т ₂=508 —273 = 235°С.

Таким образом, при нагревании баллонов с газом свыше 235 °С возможно их механическое разрушение.

Задача 2. Продукты сгорания в количестве V ₁= 4,5 м³ в топке имеют температуру t ₁ = 1200°C. Определить температуру продуктов сгорания на выходе из дымовой трубы, если известно, что их объем уменьшается в 2,8 раза (давление постоянно).

Решение. Найдем, какое количество продуктов сгорания выхо­дит из дымовой трубы:

м³.

Используя закон Гей-Люссака, определим температуру продук­тов сгорания при выходе из дымовой трубы:

К;

t = 524 – 273 = 251°С.

Задача 3. В производственном аппарате при Т =473 К газ име­ет давление p ₁ = 7 кгс/см³≈7·10⁵ Па. Какое будет давление в ап­парате, если температура продукта в аппарате повысится до 565 К.

Решение. Используя уравнение Шарля, определим

Па

или

р ₂ = 0,84 МПа.

Задача 4. Определить значение газовых постоянных в системе СИ для газов ацетилена С₂Н₂, метана СН₄и окиси углерода СО. Решение.

Для С₂Н₂ μ= 26; R = 8314/μ = 8314/26 = 319,8 Дж/(кг·К).

Для СН₄ μ = 16; R = 8314/16 = 520 Дж/(кг·К).

Для СО μ= 28; R = 8314/28 = 297 Дж/(кг·К).

Дата добавления: 2014-01-20