
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Бабич, А. А
|
|
|
|
Гомель 2011
УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ
А. А. Бабич, А. В. Емелин, Л. Д. Корсун
Дельта-сигма модуляция
Интегрирующий АЦП
Другой метод аналого-цифрового преобразования – интегрирующий – использует интегрирование для оцифровки входного сигнала. АЦП такого типа имеют ряд преимуществ – высокое разрешение, хорошую линейность и подавление помех с использованием усреднения. Однако есть и серьезный недостаток – низкая скорость преобразования. Поэтому интегрирующие АЦП преимущественно используются в качестве цифровых вольтметров или других устройств, не требующих большой частоты измерений.
Самая современная технология в АЦП – это использование дельта-сигма преобразования. АЦП такого типа используют дельта-сигма модуляторы совместно с фильтрами защиты от наложения спектров и цифровыми фильтрами. Они обеспечивают высокую частоту дискретизации, высокую точность и наилучшую линейность среди всех типов АЦП. Например, АЦП такого типа имеет разрешение 16 бит на частоте 48 кГц с полным отсутствием дифференциальной нелинейности.
Таблица А-2. Преимущества/использование различных типов АЦП
| Тип АЦП | Преимущества/использование |
| Последовательного приближения | Высокое разрешение Высокое быстродействие Легкость переключения Обычно используется на DAQ платах Может оцифровывать постоянные сигналы |
| Параллельный | Наибольшее быстродействие Отработанная технология Более дорогостоящий |
| Интегрирующий | Высокое разрешение Хорошее подавление помех Хорошая линейность Отработанная технология Низкая частота преобразования Обычно используется в цифровых мультиметрах |
| Дельта-сигма | Высокое разрешение Великолепная линейность Встроенные фильтры защиты от наложения спектров Оцифровывает переменные сигналы |
по дисциплине «Специальные математические методы и функции» для студентов дневной формы обучения
специальности 1-36 04 02 «Промышленная электроника»
УДК 517(075.8)
ББК 22.16я73
Рекомендовано к изданию научно-методическим советом
Факультета автоматизированных и информационных систем
ГГТУ им. П.О. Сухого
(протокол № 5 от 26.12.2011)
Рецензенты: зав. кафедрой «Промышленная электроника» УО ГГТУ им. П.О. Сухого к.т.н., доцент Ю. В. Крышнев,
доцент кафедры «Высшая математика» УО ГГТУ им. П.О. Сухого к.ф.-м.н., доцент Л. Л. Великович
Б- Учебно-методическое пособие по дисциплине «Специальные математические методы и функции» для студентов дневной формы обучения специальности 1-36 04 02 «Промышленная электроника» / А. А. Бабич, А. В. Емелин, Л. Д. Корсун. - Гомель: УО ГГТУ им. П. О. Сухого, 2011. - 63 с.
ПРЕДИСЛОВИЕ
Данное учебно-методическое пособие является частью комплекса учебных пособий под общим названием «Специальные математические методы и функции» и написано в соответствии с действующей программой курса «Специальные математические методы и функции», соответствующей новому образовательному стандарту и учебному плану по специальности 1-36 04 02 «Промышленная электроника». Методическое пособие адресовано студентам дневного отделения, овладевшим основами линейной алгебры и математического анализа в рамках курса «Высшая математика».
В методическом пособии весь практический материал по курсу «Специальные математические методы и функции» разбит на разделы, в каждом из которых даются необходимые сведения (основные определения, формулы), используемые при решении задач. Для проведения практических занятий и самостоятельной работы студентов в конце каждого раздела имеется задание, содержащее список задач.
Для самостоятельной подготовки к практическим занятиям и экзамену рекомендуем курс лекций по дисциплине «Специальные математические методы и функции» [1].
РАЗДЕЛ 1. Отображения множеств. Мощность множеств
Отображением f множества Х в множество Y называется всякое правило, сопоставляющее каждому элементу x множества Х единственный элемент y множества Y. При этом  называется образом
называется образом 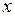 , а
, а 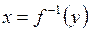 – прообразом
– прообразом 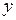 .
.
Отображение 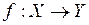 называется сюръективным или сюръекцией, если
называется сюръективным или сюръекцией, если  отображается на всё множество
отображается на всё множество 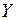 , т.е.
, т.е.  .
.
Отображение 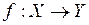 называется инъективным или инъекцией, если любым двум различным элементам
называется инъективным или инъекцией, если любым двум различным элементам  соответствуют различные образы
соответствуют различные образы  .
.
Отображение 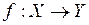 , являющееся одновременно сюръекцией и инъекцией, называется биекцией или взаимнооднозначным отображением.
, являющееся одновременно сюръекцией и инъекцией, называется биекцией или взаимнооднозначным отображением.
Множества  и
и 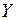 называются эквивалентными, т.е.
называются эквивалентными, т.е.  ~
~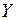 , если между ними можно установить взаимнооднозначное соответствие.
, если между ними можно установить взаимнооднозначное соответствие.
Мощностью конечного множества 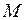 называется число его элементов
называется число его элементов  .
.
Множества А и В имеют равные мощности, если 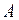 ~
~ .
.
Множество А называется счетным, если 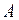 ~
~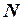 , где
, где 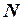 – множество натуральных чисел.
– множество натуральных чисел.
Теорема 1.1. Множество действительных чисел, принадлежащих отрезку 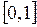 несчетно.
несчетно.
Множество 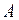 ~
~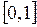 называется множеством мощности континуум.
называется множеством мощности континуум.
Мощность счетного множества обозначается символом  (алеф-нуль). Мощность мощности континуум обозначается как N (алеф) или c (готическая буква С).
(алеф-нуль). Мощность мощности континуум обозначается как N (алеф) или c (готическая буква С).
Теорема Кантора-Берштейна. Пусть А и В два произвольных множества, а  и
и 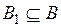 два их подмножества. Тогда если
два их подмножества. Тогда если  ~
~ и
и 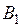 ~
~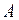 , то
, то 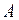 ~
~ .
.
Задания к разделу 1.
1.1. Задают ли указанные функции отображение f множество действительных чисел 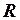 в себя, и если задают, то является ли оно сюръективным? инъективным? биективным?
в себя, и если задают, то является ли оно сюръективным? инъективным? биективным?
а) 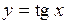 ;
;
б)  ;
;
в)  ;
;
г) 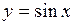 ;
;
д)  .
.
1.2. Установить, являются ли указанные отношения действующие на множествах А и В, отображением 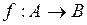 , и если являются, то будут ли они сюръективными, инъективными, биективными.
, и если являются, то будут ли они сюръективными, инъективными, биективными.
а) А – множество русских слов; B – множество букв в русском алфавите; 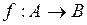 сопоставляет слову его первую букву;
сопоставляет слову его первую букву;
б) А – множество функций, непрерывных на отрезке 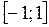 , B – множество действительных чисел;
, B – множество действительных чисел; 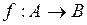 сопоставляет функции
сопоставляет функции 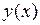 число
число  ;
;
в) А – множество функций, имеющих на отрезке 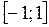 производные всех порядков;
производные всех порядков;  сопоставляет функции
сопоставляет функции  ее производную
ее производную  ;
;
г) А – множество всех окружностей плоскости; B – множество всех точек плоскости; 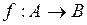 сопоставляет каждой окружности ее центр;
сопоставляет каждой окружности ее центр;
д) А – множество всех окружностей радиуса 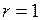 ; B – множество всех точек плоскости;
; B – множество всех точек плоскости; 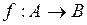 сопоставляет каждой окружности ее центр.
сопоставляет каждой окружности ее центр.
1.3. Множество А состоит из четырех элементов, а множество В из двух. Существуют ли указанные типы отображений, и если существуют, то определить их количество:
а) инъекция А в В;
б) сюръекция А на В;
в) инъекция В в А;
г) сюръекция В на А.
1.4. Построить следующие биективные отображения:
а) интервал 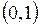 на интервал
на интервал  ;
;
б) интервал 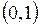 на интервал
на интервал  ;
;
в) интервал  на интервал
на интервал  ;
;
г) интервал  на интервал
на интервал  ;
;
д) интервал 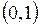 на прямую
на прямую 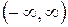 ;
;
е) интервал 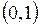 на луч
на луч  ;
;
ж) отрезок 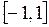 на интервал
на интервал  .
.
1.5. Отобразить множество квадратных трехчленов  , где
, где  – натуральные числа} на множество натуральных чисел, кратных 30. Существует ли биективное отображение?
– натуральные числа} на множество натуральных чисел, кратных 30. Существует ли биективное отображение?
1.6. Установить, являются ли эквивалентными множество А точек произвольного круга и множество В точек произвольного квадрата. (Указание: воспользоваться теоремой Кантора-Берштейна).
1.7. Установить, являются ли счетными следующие множества:
а) множество целых чисел Z;
б) объединение конечного числа счетных множеств;
в) объединение счетного множества счетных множеств;
г) множество рациональных чисел Q;
д) образ счетного множества при отображении f;
е) множество многочленов с целыми коэффициентами.
1.8. Показать, что множество действительных чисел имеет мощность континуум, т.е. R~ .
.
1.9. Установить мощность множества иррациональных чисел I.
1.10. Показать, что множество точек квадрата имеет мощность континуум.
1.11. Задано отображение  пространства
пространства 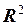 в себя. Найти:
в себя. Найти:
а) образ точки 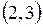 ;
;
б) образ биссектрисы первого и третьего координатных углов;
в) прообраз оси абсцисс.
1.12. Задано отображение  . Найти образ функции
. Найти образ функции  . Указать два элемента из прообраза
. Указать два элемента из прообраза  .
.
1.13. задано отображение:  пространства
пространства 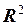 в пространство многочленов. Найти
в пространство многочленов. Найти
а) образ точки  ;
;
б) прообраз функции  ;
;
в) прообраз функции 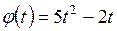 .
.
РАЗДЕЛ 2. Метрические пространства
Множество М называется метрическим пространством, если каждой паре его элементов x и y поставлено в соответствие действительное число 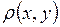 , удовлетворяющее условиям:
, удовлетворяющее условиям:
(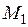 )
) 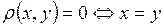 (аксиома тождества);
(аксиома тождества);
(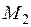 )
)  (аксиома симметрии);
(аксиома симметрии);
( )
)  (аксиома треугольника).
(аксиома треугольника).
Число 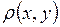 называется расстоянием между элементами x и y. Условия (
называется расстоянием между элементами x и y. Условия (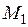 ) – (
) – ( ) называются аксиомами метрики. Элементы х метрического пространства
) называются аксиомами метрики. Элементы х метрического пространства  называются точками, а функция точек
называются точками, а функция точек 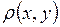 метрикой.
метрикой.
Для проверки аксиом метрики полезны следующие неравенства:
1) 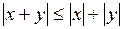 – неравенство треугольника для модуля;
– неравенство треугольника для модуля;
2) 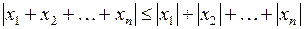 ;
;
3)  – неравенство Коши-Буняковского;
– неравенство Коши-Буняковского;
4)  , где
, где  ,
, 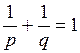 – неравенство Гёльдера;
– неравенство Гёльдера;
5)  , где
, где  –
–
неравенство Минковского;
6) 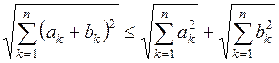 ;
;
7) 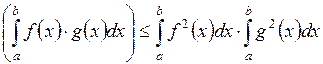 – неравенство Шварца.
– неравенство Шварца.
Множество всех точек х метрического пространства 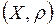 , удовлетворяющих условию
, удовлетворяющих условию  называется открытым шаром
называется открытым шаром 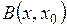 с центром в точке
с центром в точке 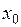 и радиусом
и радиусом  . В случае нестрогого неравенства шар называется замкнутым шаром
. В случае нестрогого неравенства шар называется замкнутым шаром  .
.
Множество М называется ограниченным, если оно целиком находится в некотором шаре.
Таблица основных метрических пространств
| Обозначение пространства | Элементы пространства | Формулы для метрик |

| 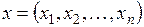
| 
|
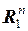
| 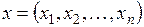
| 
|
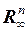
| 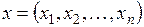
| 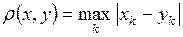
|

| 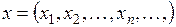 , ,
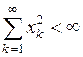
| 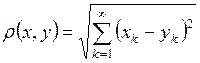
|
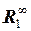
| 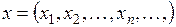 , ,
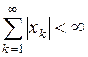
| 
|
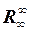
| 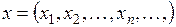 , ,
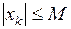 для для 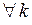
| 
|
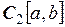
| Функция 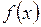 ,
непрерывная на ,
непрерывная на 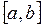
| 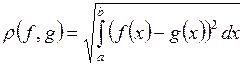
|

| Функция 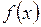 ,
непрерывная на ,
непрерывная на 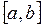
| 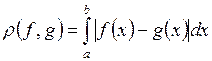
|
| Функция 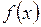 ,
непрерывная на ,
непрерывная на 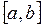
| 
|
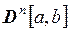
| Функция 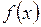 , непрерывная на , непрерывная на 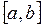 вместе со своими производными
до n -го порядка вместе со своими производными
до n -го порядка
| 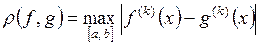 , ,

|
Задания к разделу 2.
2.1. Показать, что из аксиом метрики (М1) – (М3) следует неотрицательность метрики, т.е что  , для любых
, для любых  .
.
2.2. Доказать, что для любых четырех точек x, y, u, v метрического пространства  справедливы неравенства
справедливы неравенства
а) 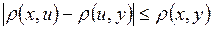 ;
;
б)  (неравенство четырехугольника).
(неравенство четырехугольника).
2.3. Доказать, что для любых  и любых
и любых 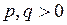 таких, что
таких, что 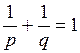 выполняется неравенство
выполняется неравенство  (неравенство Юнга).
(неравенство Юнга).
Указание: рассмотреть функции  и
и  на отрезке
на отрезке 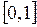 . Далее положить
. Далее положить  .
.
2.4. Доказать неравенство Гёльдера
 , где
, где 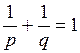 .
.
Указание: воспользоваться неравенством Юнга.
2.5. Доказать неравенство Минковского
 .
.
Указание: воспользоваться неравенством Гёльдера.
2.6. Являются ли метриками на прямой
а)  ;
;
б)  ;
;
в) 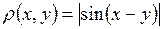 ;
;
г)  .
.
2.7. Пусть М – множество точек окружности. Зафиксируем на окружности точку 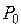 и определим расстояние между точками окружности А и В следующим образом
и определим расстояние между точками окружности А и В следующим образом

Является ли 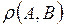 метрикой?
метрикой?
2.8. На множестве 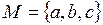 метрика задана так, что
метрика задана так, что 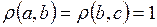 . Какие значения может принимать
. Какие значения может принимать  ?
?
2.9. Пусть  множество двоичных наборов длины n. Расстояние между двоичными наборами
множество двоичных наборов длины n. Расстояние между двоичными наборами  и
и 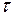 равно количеству позиций, на которых стоят различные числа. Записать формулу для
равно количеству позиций, на которых стоят различные числа. Записать формулу для  и доказать, что
и доказать, что  является метрикой (метрикой Хэмминга).
является метрикой (метрикой Хэмминга).
2.10. Образует ли метрическое пространство множество точек плоскости, если расстояние между точками 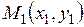 и
и  определить так
определить так
а) 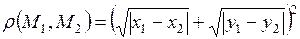 ;
;
б)  ?
?
2.11. Пусть М – множество населенных пунктов на берегу реки. Расстояние между пунктами А и В определим как время движения теплохода, имеющего собственную скорость v. Образует ли М метрическое пространство?
2.12. Задает ли метрику на пространстве многочленов формула:
а)  ;
;
б)  ?
?
2.13. Образует ли метрическое пространство множество полей максимальной длины, если за расстояние  между полями х и y принять наименьшее число ходов, которое потребуется, чтобы перейти с поля х на поле у.
между полями х и y принять наименьшее число ходов, которое потребуется, чтобы перейти с поля х на поле у.
2.14. Пусть М – метрическое пространство с метрикой  , а
, а  некоторое отображение множества А в М. Положим для любых двух точек
некоторое отображение множества А в М. Положим для любых двух точек 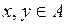
 .
.
Установить, является ли  метрикой, если отображение f
метрикой, если отображение f
а) инъективно;
б) сюръективно;
в) биективно.
2.15. Будет ли пространство непрерывных на отрезке 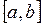 функций
функций  метрическим, если метрику определить как
метрическим, если метрику определить как
а) 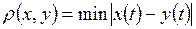 ,
,  ;
;
б)  ;
;
в)  .
.
2.16. Для множества точек плоскости  введены следующие три метрики:
введены следующие три метрики:
 ;
;
 ;
;
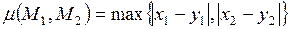 .
.
Определить их геометрический смысл и найти расстояния между точками А и В в метрических пространствах  ,
, 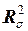 и
и  :
:
а)  ;
;
б)  .
.
2.17. Изобразить на плоскости 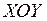
 -окрестность точки
-окрестность точки  для метрический пространств
для метрический пространств  ,
, 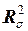 и
и  .
.
2.18. Указать на множестве клеток шахматной доски окрестности клетки 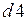 радиуса 2. для метрик, введенных в задаче 2.13.
радиуса 2. для метрик, введенных в задаче 2.13.
2.19. Найти множество точек пространства 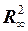 , равноудаленных от точек
, равноудаленных от точек  и
и 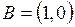 .
.
2.20. Найти множество точек пространства  , расстояние от каждой из которых до точки
, расстояние от каждой из которых до точки 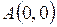 в 2 раза больше, чем расстояние до точки
в 2 раза больше, чем расстояние до точки  .
.
2.21. Найти расстояние между функциями  и
и  в метриках пространств:
в метриках пространств:
а)  ; б)
; б)  ; в)
; в)  .
.
2.22. Найти расстояние между функциями  и
и  в метриках пространств:
в метриках пространств:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 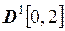 ; д)
; д) 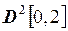 .
.
РАЗДЕЛ 3. Сходимость и непрерывность в метрических
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 970; Нарушение авторских прав?; Мы поможем в написании вашей работы!