
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пространствах
|
|
|
|
Точкой прикосновения множества Х метрического пространства М называется точка  , любая окружность которой содержит хотя бы одну точку из Х.
, любая окружность которой содержит хотя бы одну точку из Х.
Замыканием множества  называется совокупность всех его точек прикосновения. Замыкание обозначается как
называется совокупность всех его точек прикосновения. Замыкание обозначается как  .
.
Предельной точкой 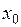 для множества
для множества  называется точка
называется точка  , всякая окрестность которой содержит по крайней мере одну точку из Х отличную от
, всякая окрестность которой содержит по крайней мере одну точку из Х отличную от 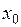 .
.
Изолированной точкой множества  называется точка, для которой найдется ее окрестность
называется точка, для которой найдется ее окрестность  , не содержащая других точек из Х.
, не содержащая других точек из Х.
Внутренней точкой множества  называется точка, для которой всегда найдется ее окрестность целиком содержащаяся в Х.
называется точка, для которой всегда найдется ее окрестность целиком содержащаяся в Х.
Внешней точкой множества  называется точка, для которой существует окрестность целиком содержащаяся в дополнении к Х, т.е. в
называется точка, для которой существует окрестность целиком содержащаяся в дополнении к Х, т.е. в 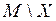 .
.
Граничной точкой множества Х называется точка, любая окрестность которой содержит как точки из Х, так и точки из его дополнения 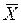 .
.
Открытым множеством называется множество, все точки которого внутренние.
Замкнутым множеством называется множество, содержащие все свои предельные точки.
Последовательность точек 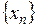 метрического пространства М сходится к точке
метрического пространства М сходится к точке 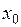 , если для любого сколь угодно малого числа
, если для любого сколь угодно малого числа 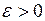 найдется номер
найдется номер 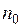 , начиная с которого все точки последовательности содержатся в
, начиная с которого все точки последовательности содержатся в  -окрестности точки
-окрестности точки 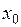 , т.е.
, т.е.  . При этом точка
. При этом точка 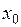 называется пределом последовательности
называется пределом последовательности 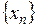 .
.
Опр.1. Отображение 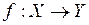 называется непрерывным в точке
называется непрерывным в точке  , если для
, если для 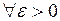
 такое, что для всех точек
такое, что для всех точек 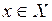 из
из  -окрестности точки
-окрестности точки 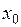 их образы
их образы 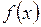 содержатся в
содержатся в  -окрестности точки
-окрестности точки  , т.е.
, т.е.
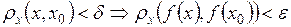 .
.
Опр.2. Отображение 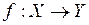 называется непрерывным в точке
называется непрерывным в точке  , если для всякой последовательности
, если для всякой последовательности 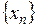 , сходящейся к
, сходящейся к 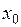 , последовательность их образов
, последовательность их образов 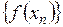 сходится к образу
сходится к образу  .
.
Последовательность точек 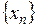 метрического пространства М называется фундаментальной или последовательностью Коши, если для любого
метрического пространства М называется фундаментальной или последовательностью Коши, если для любого 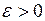 найдется номер
найдется номер 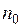 , начиная с которого расстояние между любыми точками последовательности
, начиная с которого расстояние между любыми точками последовательности 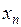 и
и 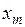 не превышает
не превышает  , т.е.
, т.е. 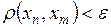 для
для 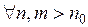 .
.
Теорема. Всякая сходящаяся в метрическом пространстве последовательность является фундаментальной.
Метрическое пространство М называется полным, если всякая фундаментальная последовательность 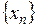 точек этого пространства сходится к точке
точек этого пространства сходится к точке 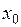 этого пространства.
этого пространства.
Задания к разделу 3.
3.1. Может ли множество, содержащее хотя бы одну граничную точку быть открытым?
3.2. Множество Х состоит из интервала 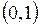 и двух изолированных точек
и двух изолированных точек 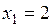 и
и 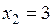 . Найти все граничные и предельные точки, а также все точки прикосновения.
. Найти все граничные и предельные точки, а также все точки прикосновения.
3.3. Множество Х состоит из точек плоскости 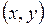 , координаты которых удовлетворяют неравенствам
, координаты которых удовлетворяют неравенствам  ,
, 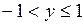 и одной изолированной точки
и одной изолированной точки 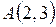 . Найти границу множества Х, а также множество предельных точек и точек прикосновения.
. Найти границу множества Х, а также множество предельных точек и точек прикосновения.
3.4. Множество Х состоит из всех точек плоскости 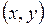 с рациональными координатами. Найти границу множества
с рациональными координатами. Найти границу множества 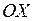 , множество всех предельных точек, а также замыкание
, множество всех предельных точек, а также замыкание  .
.
3.5. Множество  состоит из точек круга
состоит из точек круга 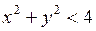 , имеющих рациональную абсциссу. Найти границу этого множества и его замыкание
, имеющих рациональную абсциссу. Найти границу этого множества и его замыкание  .
.
3.6. В метрическом пространстве 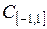 непрерывных на отрезке
непрерывных на отрезке 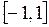 функций задано множество функций Е, удовлетворяющих условию
функций задано множество функций Е, удовлетворяющих условию 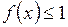 . Установить, к какому типу точек (внутренние, внешние, граничные) относятся указанные функции:
. Установить, к какому типу точек (внутренние, внешние, граничные) относятся указанные функции:
а) 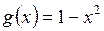 ;
;
б) 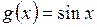 ;
;
в) 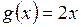 ;
;
г) 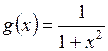 ;
;
д) 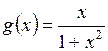 ;
;
е) 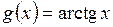 ;
;
з)  .
.
Указание: В пространстве 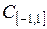 метрика вводится как
метрика вводится как 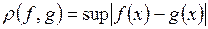 , где
, где 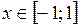 .
.
3.7. Является ли открытым множеством интервал  , если его рассматривать как подмножество:
, если его рассматривать как подмножество:
а) прямой; б) плоскости?
3.8. Является ли закрытым множеством отрезок 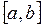 , если его рассматривать как подмножество:
, если его рассматривать как подмножество:
а) прямой; б) плоскости?
3.9. Может ли в метрическом пространстве множество быть одновременно и открытым и замкнутым?
Указание: Рассмотреть множество дискретных точек.
3.10. Является ли множество иррациональных чисел I всюду плотным в R?
3.11. Является ли всюду плотным в R множество чисел, десятичная запись которых содержит лишь цифры 1 и 2?
3.12. Доказать, что в любом метрическом пространстве М сходящаяся последовательность 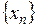 имеет единственный предел
имеет единственный предел 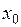 .
.
3.13. Доказать, что в любом метрическом пространстве М всякая подпоследовательность сходящейся последовательности 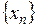 также сходится, причем к тому же пределу
также сходится, причем к тому же пределу 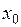 .
.
3.14. Доказать, что в метрическом пространстве всякая сходящаяся последовательность точек 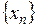 ограничена.
ограничена.
3.15. Установить, сходится ли последовательность функций 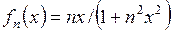 к функции
к функции  в пространствах
в пространствах
а) 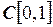 ; б)
; б)  .
.
3.16. Установить, сходится ли последовательность функций 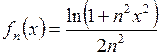 к функции
к функции  в пространстве
в пространстве 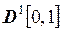 .
.
3.17. Установить, сходятся ли данные последовательности функций к функции  по метрикам указанных пространств:
по метрикам указанных пространств:
а)  ;
; 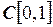 и
и  ;
;
б) 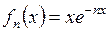 ;
; 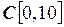 и
и  ;
;
в) 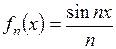 ;
; 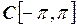 ,
, 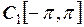 ,
, 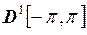 ;
;
г)  ;
; 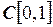 и
и  .
.
3.18. Задано отображение  подпространства Е непрерывно-дифференцируемых функций пространств
подпространства Е непрерывно-дифференцируемых функций пространств 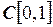 в R. Является ли это отображение непрерывным на Е?
в R. Является ли это отображение непрерывным на Е?
Указание: Рассмотреть последовательность функций 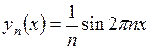 .
.
3.19. Для данных отображений 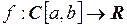 установить их непрерывность:
установить их непрерывность:
а) 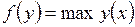 ,
, 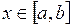 ;
;
б) 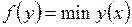 ,
, 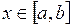 ;
;
в)  ;
;
г) 
3.20. Является ли непрерывным отображение  функционального пространства Е в пространство действительных чисел R, если
функционального пространства Е в пространство действительных чисел R, если
а) 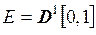 ;
;
б) 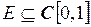 , причем функции дифференцируемы в точке 0.
, причем функции дифференцируемы в точке 0.
3.21. Задано отображение  подпространства
подпространства 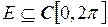 , состоящего из непрерывно дифференцируемых функций, в пространстве
, состоящего из непрерывно дифференцируемых функций, в пространстве 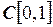 . Является ли это отображение непрерывным?
. Является ли это отображение непрерывным?
Указание: Рассмотреть последовательность функций 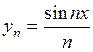 .
.
3.22. Пусть a – фиксированная точка метрического пространства М. Является ли функция 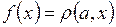 непрерывной на М?
непрерывной на М?
3.23. Установить, являются данные последовательности действительных чисел фундаментальными в R:
а) 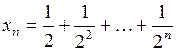 ;
;
б) 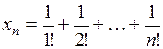 .
.
3.24. Установить, является последовательность функции 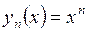 фундаментальной в указанных метрических пространствах:
фундаментальной в указанных метрических пространствах:
а) 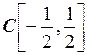 ; б)
; б) 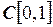 .
.
3.25. Являются ли фундаментальными данные последовательности функций в указанных пространствах:
а) 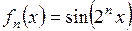 ,
, 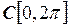 ;
;
б)  ,
, 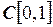 ;
;
в) 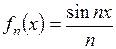 ,
, 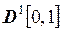 .
.
3.26. Является ли замкнутое подпространство полного метрического пространства полным?
РАЗДЕЛ 4. Принцип сжимающих отображений
Сжимающим отображением называется отображение метрического пространства М в себя 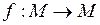 , если существует такое число q, принимающее значение
, если существует такое число q, принимающее значение  , что для любых двух точек х и у из М выполняется неравенство
, что для любых двух точек х и у из М выполняется неравенство
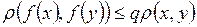 .
.
Неподвижной точкой отображения 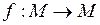 называется точка х из М такая, что
называется точка х из М такая, что
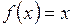 .
.
Принцип сжимающих отображений. Всякое сжимающее отображение, определенное в полном метрическом пространстве, имеет единственную неподвижную точку.
Для сжимающего отображения 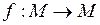 справедлива следующая оценка сходимости последовательности приближений
справедлива следующая оценка сходимости последовательности приближений 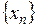 к неподвижной точке х:
к неподвижной точке х:
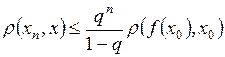 ,
,
где 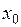 – стартовая точка.
– стартовая точка.
Критерий сжимаемости отображения. Дифференцируемая функция 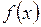 сжимающее на отрезке
сжимающее на отрезке 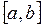 отображение, если на этом отрезке
отображение, если на этом отрезке  .
.
При этом на отрезке 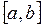 имеется одна неподвижная точка.
имеется одна неподвижная точка.
Неподвижная точка может быть обнаружена с помощью метода итераций: 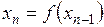 .
.
Задания к разделу 4.
4.1. найти неподвижные точки отображения  числовой прямой в себя.
числовой прямой в себя.
4.2. Установить, имеет ли отображение
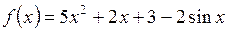
числовой прямой в себя неподвижные точки.
4.3. найти неподвижные точки данного отображения  :
:
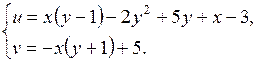
4.4. Найти неподвижные точки отображения

пространства 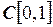 в себя.
в себя.
4.5. Найти неподвижные точки отображения 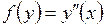 пространства дважды дифференцируемых функций в себя.
пространства дважды дифференцируемых функций в себя.
4.6. Установить, задает ли функция  , определенная на отрезке
, определенная на отрезке 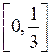 , сжимающее отображение.
, сжимающее отображение.
4.7. Установить, задает ли функция 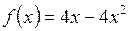 , определенная на отрезке
, определенная на отрезке 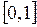 , сжимающее отображение.
, сжимающее отображение.
4.8. Является ли сжимающим отображение 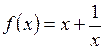 луча
луча  в себя?
в себя?
4.9. Является ли сжимающим отображение 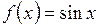 числовой прямой в себя.
числовой прямой в себя.
4.10. Является ли сжимающим отображение 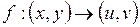 , где
, где
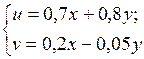
плоскости в себя, если плоскость рассматривается как метрическое пространство: а) 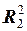 ; б)
; б)  .
.
4.11. Является ли отображение 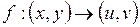 , где
, где
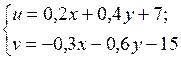
плоскости в себя сжимающим, если плоскость рассматривается как метрические пространства: а) 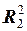 ; б)
; б)  ; в)
; в) 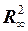 .
.
4.12. Установить, является ли отображение 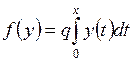 пространства
пространства 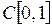 в себя сжимающим, если
в себя сжимающим, если  .
.
4.13. Установить, имеют ли последовательности, заданные рекуррентными соотношениями, неподвижные точки, и если имеют, то найти их
а)  ,
, 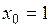 ;
;
б) 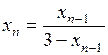 ,
, 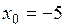 ;
;
в) 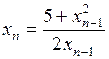 ,
, 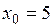 .
.
Указание: Ввести соответствующее отображение 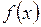 , определить область, в которой
, определить область, в которой 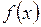 является сжимающим отображением. Предел найти как неподвижную точку.
является сжимающим отображением. Предел найти как неподвижную точку.
4.14. Установить, является ли последовательность дробей
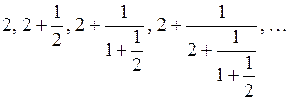
сходящейся, и если является, то найти ее предел.
4.15. Доказать, что следующие последовательности имеют пределы и найти их:
а) 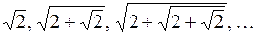 ;
;
б)  .
.
РАЗДЕЛ 5. Линейное пространство
Линейным пространством V над полем действительных или комплексных чисел  называется непустое множество, любой паре элементов которого
называется непустое множество, любой паре элементов которого 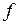 и
и 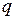 при помощи операций сложения и умножения на числе
при помощи операций сложения и умножения на числе 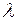 ставятся в соответствие единственные элементы
ставятся в соответствие единственные элементы 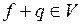 и
и 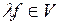 со свойствами:
со свойствами:
V1: 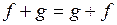 (коммутативность)
(коммутативность)
V2: 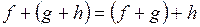 (ассоциативность)
(ассоциативность)
V3: 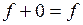 (существование элемента 0)
(существование элемента 0)
V4: 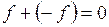 (существование элемента
(существование элемента 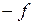 )
)
V5: 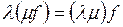 (ассоциативность)
(ассоциативность)
V6:  (дистрибутивность)
(дистрибутивность)
V7: 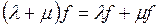 (дистрибутивность)
(дистрибутивность)
V8: 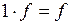
Элементы линейного пространства V называются точками или векторами. Часто линейное пространство V называют векторным пространством.
Линейно независимой называется система векторов 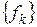 ,
, 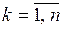 , если их линейная комбинация обращается в 0 только при нулевых коэффициентах:
, если их линейная комбинация обращается в 0 только при нулевых коэффициентах:
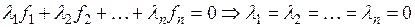 .
.
В противном случае система называется линейно зависимой.
Бесконечная система векторов называется независимой, если любая ее конечная подсистема линейно независима.
Конечномерным линейным пространством V называется линейное пространство, имеющее систему из n линейно независимых векторов, причем всякая система, содержащая 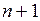 вектор должна быть линейно зависимой. При этом число n называется размерностью
вектор должна быть линейно зависимой. При этом число n называется размерностью 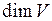 относительно линейного пространства V.
относительно линейного пространства V.
Базисом линейного пространства V размерности  называется любая совокупность n линейно независимых векторов.
называется любая совокупность n линейно независимых векторов.
Координатами вектора  в базисе
в базисе 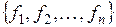 называются координаты
называются координаты 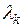 ,
, 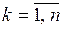 разложения вектора
разложения вектора  по базису
по базису 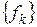 :
:
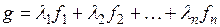 .
.
Линейным подпростанством Е векторного пространства V называется непустое подмножество 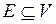 , которое замкнуто относительно операций сложения векторов и умножения на член
, которое замкнуто относительно операций сложения векторов и умножения на член 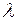 из поля R или C.
из поля R или C.
Линейной оболочкой 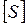 системы векторов
системы векторов 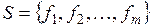 линейного пространства V называется множество всех их возможных линейных комбинаций
линейного пространства V называется множество всех их возможных линейных комбинаций
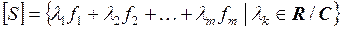 .
.
Векторной суммой 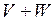 линейных пространств V и W называется множество всех векторов, представленных в виде
линейных пространств V и W называется множество всех векторов, представленных в виде
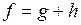 , где
, где 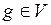 ,
, 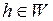 .
.
Прямой векторной суммой  линейных пространств V и W называется их сумма
линейных пространств V и W называется их сумма 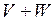 при условии, что
при условии, что 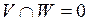 .
.
Размерность суммы двух конечномерных векторов пространств V и W может быть найдена по формуле Грассмана:
 .
.
Прямым произведением 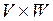 векторных пространств V и W называется множество всех упорядоченных пар векторов
векторных пространств V и W называется множество всех упорядоченных пар векторов  ,
,  ,
, 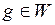 , на котором определены следующие операции сложения и умножения на число
, на котором определены следующие операции сложения и умножения на число  :
:
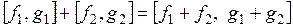 ,
,
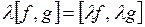 .
.
Выпуклым множеством S называется подмножество  , если для любой пары его элементов
, если для любой пары его элементов  для произвольного числа
для произвольного числа 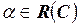 справедливо включение
справедливо включение
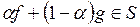 .
.
Выпуклой оболочкой 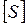 называется наименьшее подмножество V, содержащее S.
называется наименьшее подмножество V, содержащее S.
Задания к разделу 5.
5.1. Является ли линейным пространство
а) пустое множество 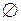 ;
;
б) множество, состоящее из одного нулевого элемента.
5.2. Существует ли линейное пространство, состоящее только из двух элементов?
5.3. Являются ли линейными пространствами над полем R множества:
а) рациональных чисел;
б) иррациональных чисел?
5.4. Являются ли линейными пространствами над полем С множества:
а) рациональных чисел;
б) иррациональных чисел?
5.5. Установить, являются ли линейными подпространствами заданные множества векторов в n мерном векторном пространстве V, и если являются, то найти их размерность:
а) множество векторов, все координаты которых равны между собой;
б) множество векторов, первая координата которых равна 0;
в) множество векторов, сумма координат которых равна 0;
г) множество векторов, сумма координат которых равна 1;
д) множество векторов плоскости, параллельных между собой;
е) множество векторов трехмерного пространства, перпендикулярных данной прямой;
ж) множество векторов плоскости, модули которых не превышают 1;
з) множество векторов плоскости, образующих угол 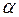 с заданной прямой.
с заданной прямой.
5.6. Установить, является ли заданное множество квадратных матриц порядка n линейным подпространством в пространстве всех квадратных матриц порядка n, и если является, то найти его размерность:
а) множество матриц с нулевой первой строкой;
б) множество диагональных матриц;
в) множество верхних треугольных матриц;
г) множество симметричных матриц;
д) множество антисимметричных матриц;
е) множество вырожденных матриц.
5.7. Установить, образует ли данное множество функций на произвольном отрезке 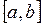 линейное пространство относительно обычных операций сложения и умножения на действительное число
линейное пространство относительно обычных операций сложения и умножения на действительное число 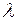 :
:
а) множество непрерывных функций;
б) множество дифференцируемых функций;
в) множество интегрируемых функций;
г) множество ограниченных функций;
д) множество функций таких, что  ;
;
е) множество неотрицательных функций;
ж) множество функций таких, что 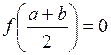 ;
;
з) множество функций таких, что 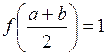 ;
;
и) множество функций таких, что 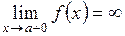 ;
;
к) множество монотонно возрастающих функций.
5.8. Доказать, что при любом натуральном n данное множество функций образует конечномерное линейное пространство. Найти размерность и указать базис этого пространства:
а) множество многочленов степени 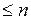 ;
;
б) множество четных многочленов степени 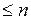 ;
;
в) множество нечетных многочленов степени 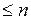 ;
;
г) множество тригонометрических многочленов порядка 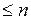 вида
вида
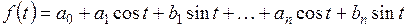 ;
;
д) множество четных тригонометрических многочленов порядка не выше n;
е) множество нечетных тригонометрических многочленов порядка не выше n;
ж) множество функций вида
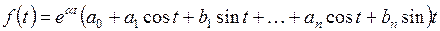 .
.
5.9. Найти размерность и базис линейной оболочки заданной системы столбцов:
а) 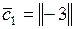 ,
,  ;
;
б) 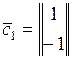 ,
,  ,
,  ;
;
в) 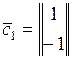 ,
,  ,
, 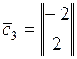 ;
;
г)  ,
, 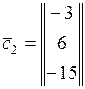 ,
, 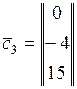 .
.
5.10. Найти размерность и базис линейной оболочки системы матриц:
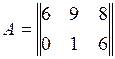 ,
, 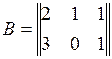 ,
, 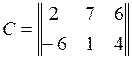 .
.
5.11. Найти размерность и базис линейной оболочки системы многочленов
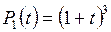 ;
; 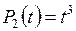 ;
; 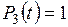 ;
; 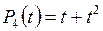 .
.
5.12. Показать, что многочлены 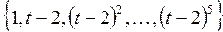 образуют базис в пространстве многочленов степени не выше 5 и найти координаты заданных многочленов в этом базисе:
образуют базис в пространстве многочленов степени не выше 5 и найти координаты заданных многочленов в этом базисе:
а) 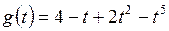 ;
;
б) 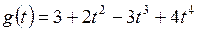 ;
;
в)  ;
;
г) 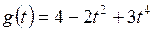 ;
;
д)  .
.
5.13. Доказать, что пространство квадратных матриц порядка n является прямой суммой подпространства симметричных и антисимметричных матриц.
5.14. Установить, является ли n -мерное арифметическое пространство 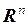 прямой суммой продпространства векторов, координаты которых равны между собой, и подпространства векторов, сумма координат которых равна 0.
прямой суммой продпространства векторов, координаты которых равны между собой, и подпространства векторов, сумма координат которых равна 0.
5.15. Найти размерность и базис суммы и пересечения линейных подпространств, натянутых на системы векторов 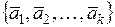 и
и  :
:
а) 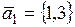 ,
, 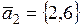 ,
, 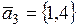 ;
;
 ,
,  ,
,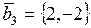 ;
;
б) 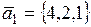 ,
, 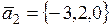 ,
, 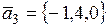 ;
;
 ,
,  ,
,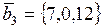 .
.
5.16. Найти размерность и базис суммы и пересечения линейных подпространств пространства многочленов степени не выше 3, натянутых на системы многочленов
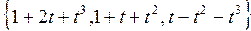 и
и 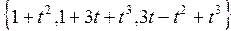 .
.
РАЗДЕЛ 6. Нормированные линейные пространства
Нормой элемента f линейного пространства V называется действительное число  , удовлетворяющее следующим условиям:
, удовлетворяющее следующим условиям:
Н1: 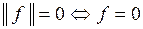 ;
;
Н2: 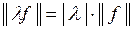 для
для 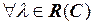 ;
;
Н3: 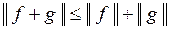 для
для 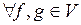 .
.
Нормированным линейным пространством называется линейное пространство с введенной в ней нормой  .
.
Всякое нормированное пространство является метрическим. Метрика вводится по формуле
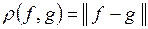 .
.
Таблица основных нормированных пространств
| Обозначение пространства | Элементы пространств | Формулы для норм |

| 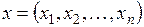
| 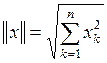
|
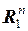
| 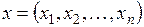
| 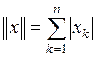
|
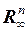
| 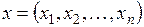
| 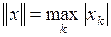
|

| 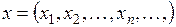 , ,
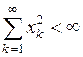
| 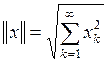
|
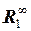
| 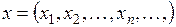 , ,
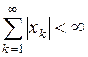
| 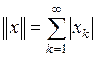
|
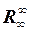
| 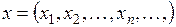 , ,
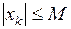
| 
|
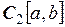
| непрерывная
на 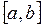 функции функции
| 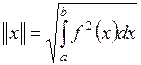
|

| непрерывная
на 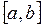 функции функции
| 
|
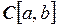
| непрерывная
на 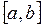 функции функции
|  , , 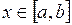
|
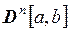
| непрерывная вместе со своими производными до n -го порядка функция |  , ,

|
Задания к разделу 6.
6.1. Является ли отображение  векторного пространства в множество неотрицательных действительных чисел, определенное как
векторного пространства в множество неотрицательных действительных чисел, определенное как 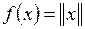 сюръективным?
сюръективным?
6.2. Задают ли метрику на числовой прямой следующие функции:
а) 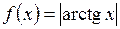 ;
;
б)  ;
;
в) 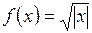 ;
;
г) 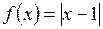 ;
;
д) 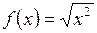 ;
;
е) 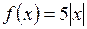 ;
;
ж)  .
.
6.3. Пусть Е – множество векторов 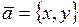 на плоскости, заданных своими декартовыми координатами. Задают ли на Е норму
на плоскости, заданных своими декартовыми координатами. Задают ли на Е норму 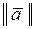 следующие функции:
следующие функции:
а) 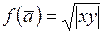 ;
;
б) 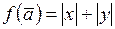 ;
;
в) 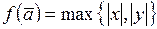 ;
;
г) 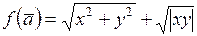 .
.
6.4. Пусть P – линейное пространство многочленов с действительными коэффициентами. Можно ли принять за норму на Р:
а) модуль значения многочлена в точке 0;
б) сумму модулей коэффициентов многочлена.
6.5. Доказать, что пространство 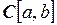 является нормированным.
является нормированным.
6.6. Найти норму функции 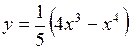 в пространствах:
в пространствах:
а) 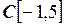 ; б)
; б)  ; в)
; в) 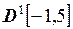 .
.
6.7. Найти норму последовательности 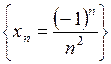 в пространствах:
в пространствах:
а)  ; б)
; б) 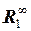 ; в)
; в) 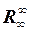 .
.
6.8. Показать, что в нормированном пространстве никакая сфера 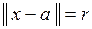 не может быть пустым множеством.
не может быть пустым множеством.
РАЗДЕЛ 7. Евклидовы пространства. Ортогональность. Процедура Грамма-Шмидта. Гильбертово пространство.
Евклидовым пространством Е называется линейное пространство V, наделенное скалярным произведением.
Скалярным произведением называется функционал, действующий из  в R, удовлетворяющий следующим свойствам:
в R, удовлетворяющий следующим свойствам:
1.  , причем
, причем 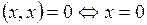 ;
;
2. 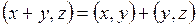 ;
;
3. 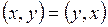 ;
;
4. 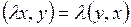
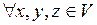 и
и 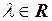 .
.
Для любых двух элементов 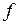 и
и  евклидова пространства имеет место неравенство Коши-Буняковского:
евклидова пространства имеет место неравенство Коши-Буняковского:
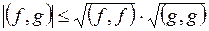
Любое евклидово пространство является нормированным с нормой  .
.
Ортогональными называются два элемента х и у евклидова пространства, если их скалярное произведение равно 0.
Угол между элементами евклидова пространства определяется через равенство
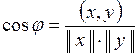 .
.
Ортонормированной называется система ненулевых векторов 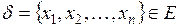 , если
, если
1. 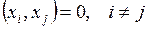 ;
;
2.  .
.
Система ортогональных векторов линейно независима. Для системы ортогональных векторов справедлива теорема Пифагора:
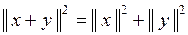 .
.
Если в некотором евклидовом пространстве существует линейно-независимая система векторов 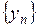 , тогда ортонормированную систему векторов
, тогда ортонормированную систему векторов 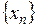 можно получить используя процедуру Грамма-Шмидта:
можно получить используя процедуру Грамма-Шмидта:
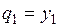 ;
; 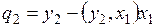 ; …;
; …;  .
.
 ;
; 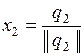 ; …;
; …; 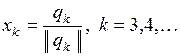
Гильбертовым пространством называется полное евклидово пространство.
Задания к разделу 7.
1. Пусть 
 . Доказать, что
. Доказать, что 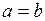 .
.
2. Является ли евклидовым пространством 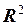 , если паре векторов
, если паре векторов  ,
, 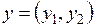 поставлено в соответствие число:
поставлено в соответствие число:
а) 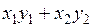 ; б)
; б)  ;
;
в) 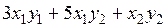 ; г)
; г) 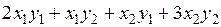 .
.
3. Является ли евклидовым пространством 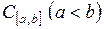 , если каждой паре функций
, если каждой паре функций 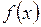 ,
, 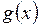 этого пространства поставлено в соответствие число:
этого пространства поставлено в соответствие число:
а)  ; б)
; б) 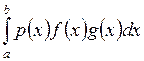 .
.
4. а) Найти длину вектора 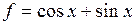 , если
, если 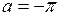 ,
, 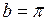 ;
;
б) 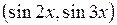 ,
, 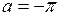 ,
, 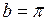 ;
;
в) 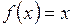 ,
, 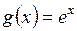 ,
, 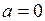 ,
,  ;
;
г) угол между векторами 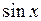 и
и 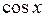 ,
, 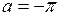 ,
, 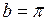 .
.
5. Являются ли ортогональными в евклидовом пространстве следующие системы векторов:
а)  ,
, 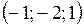 ,
, 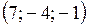 ;
;
б)  ,
, 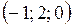 ,
, 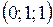 .
.
6. Пронормировать следующие векторы, заданные координатами в ортонормированном базисе:
а) 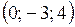 , б)
, б)  , в)
, в)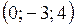 .
.
7. Какие из данных систем векторов являются ортогональными в 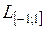 :
:
а) 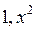 ; б)
; б) 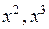 ; в)
; в) 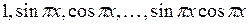 .
.
8. В евклидовом пространстве 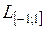 пронормировать следующие векторы:
пронормировать следующие векторы:
а) 1; б)  ; в)
; в) 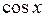 .
.
9. В евклидовом пространстве 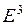 даны два ортогональных вектора а и
даны два ортогональных вектора а и 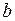 . Найти вектор с, такой, что а,
. Найти вектор с, такой, что а, 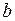 , с образуют ортонормированный базис, если
, с образуют ортонормированный базис, если
а)  ;
; 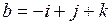 ;
;
б)  ;
;  .
.
10. В евклидовых пространствах 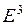 ,
, 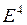 по данному базису построить ортонормированный
по данному базису построить ортонормированный
а) 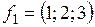 ,
, 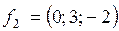 ,
, 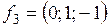 ;
;
б)  ,
, 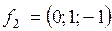 ,
, 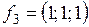 ;
;
а) 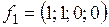 ,
,  ,
,  ,
, 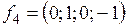 .
.
11. В евклидовом пространстве многочленов степени не выше первой, рассматриваемых на отрезке 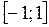 по данному базису
по данному базису  ,
, 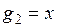 построить ортонормированный.
построить ортонормированный.
РАЗДЕЛ 8. Линейные операторы в евклидовых пространствах. Спектр собственных значений линейных операторов. Обратимость.
Пусть V и W два линейных пространства. Всякое отображение А, составляющее каждому элементу  единственный элемент
единственный элемент 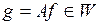 , называется оператором, действующим из V в W.
, называется оператором, действующим из V в W.
Линейным называется оператор А, если
1) 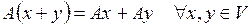 ;
;
2) 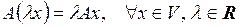 .
.
В конечномерном пространстве V линейный оператор задается квадратной матрицей 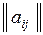 . И наоборот, всякая квадратная матрица определяет в соответствующем пространстве линейный оператор или линейное преобразование.
. И наоборот, всякая квадратная матрица определяет в соответствующем пространстве линейный оператор или линейное преобразование.
Пусть Е – комплексное векторное пространство. Собственным значением оператора А называется комплексное число 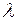 :
: 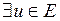 ,
, 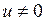 , такой что
, такой что
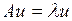 . (1)
. (1)
Собственным вектором оператора А, соответствующим собственному значению 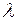 называется всякий вектор
называется всякий вектор 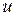 , удовлетворяющий соотношению (1).
, удовлетворяющий соотношению (1).
В конечномерных пространствах уравнение (1) эквивалентно системе линейных уравнений
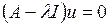 , (2)
, (2)
где I – единичная матрица.
Для того, чтобы система (2) имела ненулевые решения, она должна быть вырожденной, а значит
 - характеристическое уравнение. (3)
- характеристическое уравнение. (3)
Это уравнение имеет n корней.
Каждому собственному вектору соответствует единственное собственное значение, но существует бесконечное множество векторов для заданного собственного значения.
Резольвентой линейного оператора А называется оператор 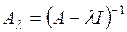 . Значения
. Значения 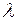 , для которых
, для которых 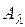 определен и однозначен, называются регулярными точками А. Множество всех чисел
определен и однозначен, называются регулярными точками А. Множество всех чисел 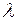 , которые не являются регулярными, называются спектром А.
, которые не являются регулярными, называются спектром А.
Множество всех собственных значений А, которые являются подмножеством спектра А, называется точечным спектром.
Для конечномерных пространств спектр линейного оператора А состоит только из точечного спектра.
Оператор В, определенный на R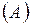 называется обратным к А оператором, если выполняются условия:
называется обратным к А оператором, если выполняются условия:

 R
R 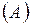 , R
, R 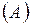 – область значений
– область значений
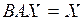
 D
D 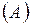 , D
, D 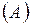 – область определения.
– область определения.
Обратимым называется оператор, который имеет обратный. Обратный оператору А обозначается 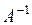 .
.
Задания к разделу 8.
1. Является ли линейным оператор 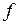 :
: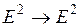 , если
, если 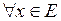
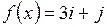 .
.
2. Может ли линейный оператор перевести пару ненулевых коллинеарных векторов в пару неколлинеарных?
3. Каков геометрический смысл условий линейности оператора
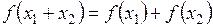 ,
,  .
.
4. Является ли линейным каждый из операторов 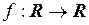 , заданный следующим образом:
, заданный следующим образом: 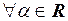
а) 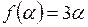 ; б)
; б) 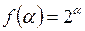 ; в)
; в) 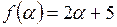 ;
;
г)  ; д)
; д) 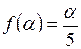 .
.
5. Является ли линейным оператор 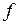 , переводящий всякий вектор
, переводящий всякий вектор 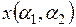 в вектор
в вектор 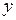 , заданный координатами в том же базисе, если:
, заданный координатами в том же базисе, если:
а)