Элементарные функции, логические связки

Помимо табличного вторым основным способом задания функций алгебры логики является их формульное построение при помощи ограниченного набора исходных простых базовых функций, называемых элементарными. Рассмотрим их.

Константы. Функции, определенные при любом числе переменных n и принимающие на всех наборах только одно значение истинности - либо только 0 либо только 1.

1-местные функции, не являющиеся константами. Обозначив переменную в них х, получим следующие две таблицы истинности:

x	f 1	f 2

Функцию f ₁ называют тождественной. Обозначают: f ₁(х)= х. Функцию f ₂ называют отрицание (инверсия). Обозначают: f ₂(х)=Ø х либо f ₂(х)= `х.

Тождественная функция сохраняет логическое значение переменной. Отрицание изменяет значение аргумента на противоположное: Ø1=0; Ø0=1.

2-местные функции. Рассмотрим 2-местные функции, принятые в качестве элементарных.

1. Конъюнкция (логическое умножение) двух логических величин х и у истинна только тогда, когда они обе истинны, т.е. х = у = И. Иначе конъюнкция ложна. Обозначают конъюнкцию как: &; Ù; ×; min; AND. Таблица истинности конъюнкции имеет вид:

x	y	&

2. Дизъюнкция (логическое сложение) двух логических величин х и у истинна во всех случаях, когда истинна хотя бы одна из них. Дизъюнкция ложна только в случае х = у = Л. Обозначают дизъюнкцию как: Ú; +; max; OR. Таблица истинности ее:

x	y	Ú

Также дизъюнкцию называют нестрогим (неисключающим) сложением.

3. Импликация (логическое следование) двух логических величин х и у означает правильный вывод величины у из х. Обозначается: ®; É; IMP. Таблица истинности импликации имеет вид:

x	Y	®

Он обусловлен тем, что, правильно рассуждая, из лжи можно вывести все, что угодно, а из истины – только истину. Верно рассуждая, нельзя только вывести из истины ложь, т.е. (1 ® 0) = 0 = Л. Лишь в случае х =1 и у =0 рассуждение не может быть правильным.

4. Эквивалентность двух логических величин х и у означает, что значения х и у совпадают: х = у. Обозначается: º; «; Ê; EQV. Таблица истинности эквивалентности следующая:

x	Y	º

5. Сложение по модулю 2 (строгое, исключающее сложение). Отличается от нестрого логического сложения (дизъюнкции) тем, что оно ложно при х = у = И. Истинность данной операции для произвольных х и у совпадает с истинностью соотношения: х ¹ у. Обозначают сложение по модулю 2как: Å; ХОR. Таблица истинности имеет вид:

x	Y	Å

6. Функция Шеффера (штрих Шеффера, антиконъюнкция, НЕ-И) – отрицание конъюнкции. Функция ложна только тогда, когда обе ее переменных истинны, т.е. при х = у = И. Иначе функция дает значение “истина”. Обозначают функцию Шеффера как: ï. Таб­лица истинности:

x	Y	ï

7. Функция Пирса (стрелка Пирса, функция Вебба, антидизъюнкция, НЕ-ИЛИ) – отрицание дизъюнкции. Функция истинна только тогда, когда обе ее переменных ложны, т.е. при х = у = Л. Иначе функция дает значение “ ложь”. Обозначают функцию Пирса как: ¯. Таблица истинности:

x	Y	¯

8. Коимпликация (антиимпликация) - отрицание импликации. Обозначается: . Таблица истинности коимпликации:

x	Y

Символы Ø, &, Ú, Å, º, ®, |, ¯, 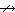, обозначающие элементарные функции, называют логическими связками. С их помощью логические функции могут быть заданы в виде формул - записей специального вида.

Для упрощения записи выражений с помощью логических связок приняты следующие соглашения об их силе:

1) Ø – самая сильная (при отсутствии скобок применяется ранее других),

2) & – вторая по силе,

3) связки Ú, Å, ®, |, ¯, 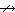равносильны,

4) связка º самая слабая.

Равные по силе связки выполняются слева – направо.

Функции 0, 1, Ø, &, Ú, Å, º, ®, |, ¯, 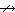, называют элементарными. При помощи этих функций можно выразить все более сложные n -местные функции алгебры логики (n ³2).

Элементарными пороговыми называют функции одной и двух переменных, логическое значение которых постоянно (равно 0 или 1) на всех наборах переменных, кроме самого первого по порядку набора (где все переменные равны 0) либо самого последнего (где переменные равны 1). На этом наборе функция ровно один раз меняет свое логическое значение (0 – на 1, 1 – на 0).

Данные функции имеют простую физическую реализацию и поэтому широко используются при конструировании цифровых вы­числительных и управляющих устройств. К пороговым относятся обе одноместные функции ― тождественная функция х и отрицание `х.

Среди двуместных пороговыми являются 4 функции:

1) конъюнкция &,

2) дизъюнкция Ú,

3) штрих Шеффера |,

4) функция Пирса ¯.

Пороговый (скачкообразный) принцип действия рассмотренных двухместных функций &, Ú, |, ¯ позволяет ввести их аналоги на случай произвольного числа переменных n.

Обобщенными пороговыми называют следующие n – местные функции:

1) обобщенная конъюнкция &(`х <sup>n</sup>), равная 1 при `х ⁿ = (1, 1,..., 1)и 0 на всех остальных наборах,

2) обобщенная дизъюнкция Ú (`х <sup>n</sup>), равная 0 при `х ⁿ = (0, 0,..., 0)и 1 на всех остальных наборах,

3) обобщенная функция Шеффера | (`х <sup>n</sup>), равная 0 при `х ⁿ = (1, 1,..., 1) и 1 на всех остальных наборах,

4) обобщенная функция Пирса ¯ (`х <sup>n</sup>), равная 1 при `х ⁿ =(0, 0,..., 0)и 0 на всех остальных наборах.

Логические связки, обозначающие элементарные и обобщенные функции, свойства которых хорошо известны, являются “кирпичиками”, при помощи которых можно в символьном виде представить логические функции.

Дата добавления: 2014-01-20