Логические формулы, их связь с логическими функциями

Роль формул в каждой научной дисциплине заключается в описании ее объектов, а также операций, выполняемых с ними. Совокупность всех формул теории составляет ее формальный язык. Обычно формулы представляют собой линейную запись специального (не произвольного!) вида, состоящую из символов, применение которых допускается в данной дисциплине. Формулу в логике можно определить следующим образом.

Логической формулой называют записи вида:

а) х, где х – логическая переменная;

б) а, где а – логическая константа;

в) Ø F ₁, F ₁& F ₂, F ₁Ú F ₂, F ₁® F ₂, F ₁º F ₂, F ₁Å F ₂, F ₁¯ F ₂, F ₁ï F ₂, F ₁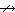 F ₂, где F ₁, F ₂ – логические формулы.

г) h (F ₁, …, F_n), где n > 2, F ₁, …, F_n ― логические формулы, h ―обозначение обобщенной пороговой функции.

Замечание. Не всякая запись, содержащая обозначения переменных, констант, логических связок, а также скобки, является формулой.

Пример 1:

а) записи х &Ø(у ® z); Ø uÚ Ø z & b; |(x, a, z Ú u) являются логическими формулами, поскольку удовлетворяют данному выше определению;

б) запись ® х &(у | z) не является логической формулой, поскольку неправильно применена операция ® (импликация), которая должна соединять два аргумента;

в) запись х Ø у не является логической формулой, поскольку в ней неправильно применена операция отрицания Ø.

С точки зрения свойств логической формулы наименование входящих в нее переменных не имеет значения. Существенно лишь то, являются ли эти переменные независимыми или на них наложе­ны дополнительные связи – например, одна из них является функцией других.

Функцией, реализуемой формулой F, называют функцию, т.е. отображение, получаемое при подстановке значений переменных в F. Обозначим ее f (F).

Каждая формула F имеет единственную функцию f (F), реализующую ее. Функция f (F) однозначно определяется, например, своей таблицей истинности.

Пример 2. Рассмотрим, например, формулу F = ху Å(х ® z). Для того, чтобы построить таблицу истинности реализуемой функции f (F), необходимо последовательно с учетом силы логических связок для всех наборов переменных выполнить логическое умножение xy, затем импликацию (х ® z), после чего сложить полученные значения истинности по модулю 2. Результат выполнения действий показан в таблице:

x	y	z	xy	х ® z y	f

Помимо построения полной таблицы истинности формула позволяет находить значения соответствующей ей функции и для отдельных наборов значений ее переменных.

Пример 3. Для функции f (x, y, z), реализующей логическую формулу F = ху Å(х ® z), найти значения истинности при следующих значениях ее переменных: а) x =0, y =1, z =0, б) x =1, y =0, z =0.

Решение. Подстановки выполняем последовательно с уче­том силы логических связок:

а) f (0, 1, 0)=0&1Å(0®0)=0Å1=1,

б) f (1, 0, 0)=1&0Å(1®0)=0Å0=0.

Ответ: а) f (0, 1, 0)=1,б) f (1, 0, 0)=0.

Пример 4. Дан фрагмент таблицы истинности выражения F, зависящего от переменных X, Y, Z:

X	Y	Z	F

Определить возможный формульный вид F:

1) X ÙY ÙZ 2) ØX ÚØY ÚZ 3) X ÚY ÚZ 4) X ÙY ÙØZ

Решение. Задача может быть решена построением как полных так и частичных таблиц истинности для функций, реализующих формулы 1)- 4) и проверкой их значений на заданных наборах.

Однако меньшее число операций затрачивается при последо­вательной подстановке в них наборов переменных и исключением вариантов формул, которые не удовлетворяют условию задачи.

I. X =1, Y =0, Z =1. F =1.

1) 1Ù0Ù1=0 ¹1 – вариант 1 не удовлетворяет;

2) Ø1 ÚØ0 Ú1 = 1– вариант 2 удовлетворяет;

3) 1 Ú0 Ú1 = 1– вариант 3 удовлетворяет;

4) 1 Ù0 ÙØ1 = 0 ¹1 – вариант 4 не удовлетворяет.

После подстановки первого набора значений переменных X =1, Y =0, Z =1 варианты ответа 1) и 4) можно отбросить.

II. X =1, Y =1, Z = 0. F =1. Проверяем только варианты 2) и 3):

2) Ø1 ÚØ1 Ú0 = 1– вариант 2 удовлетворяет;

3) 1 Ú1 Ú0 = 1– вариант 3 также удовлетворяет.

III. X =1, Y =1, Z = 1. F =1. Проверяем варианты 2) и 3):

2)1Ù1ÙØ1=0¹1– вариант 2 не удовлетворяет;

3) 1 Ú1 Ú1 = 1– вариант 3 удовлетворяет.

Всем условиям удовлетворяет только формула 3).

Ответ: X Ú Y Ú Z.

Областью истинности функции f (x, y,…), реализующей формулу F (x, y,…), называют все множество наборов ее переменных (x, y,…), на которых данная функция истинна, т.е. выполняется условие f (x, y, …) =1.

В рассмотренном выше примере 2 для функции f (F), реализующей формулу F = ху Å(х ® z), областью истинности являются следующие наборы переменных (x, y, z): (0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 1), (1, 1, 0).

В общем случае между логическими формулами и функциями выполняются следующие соотношения.

1. По заданной формуле реализуемая функция определяется однозначно (например, путем построения таблицы истинности),

2. По заданной с помощью таблицы функции соответствующую ей формулу можно построить неединственным образом.

Пример 5. Определить, для какого из предложенных слов истинно высказы­вание: Ø(Первая буква слова согласная®(Вторая буква слова гласная Ú Последняя буква слова гласная)): 1) ГОРЕ; 2) ПРИВЕТ; 3) КРЕСЛО; 4) ЗАКОН.

Решение. Заданное высказывание истинно одновременно с ложностью противоположного ему высказывания:

Первая буква слова согласная®(Вторая буква слова гласная Ú Последняя буква слова гласная).

Это высказывание по свойству импликации ложно только в том случае, когда первый аргумент истинный, а второй ложный:

1) Первая буква слова согласная = 1;

2) Вторая буква слова гласная Ú Последняя буква слова гласная = 0.

Условие 1) выполняется для всех слов.

Составное высказывание 2) по свойству логического сложения выполняется только тогда, когда ложны оба входящих в него простых высказывания, т.е. одновременно справедливо:

Вторая буква слова гласная = 0;

Последняя буква слова гласная = 0.

Из этих условий следует, что в слове должны быть согласными вторая и последняя буквы. Этому условию отвечает только слово ПРИВЕТ (2 вариант ответа).

Ответ: ПРИВЕТ.

Задачу из примера 5 можно было бы решить поочередной подстановкой всех слов в заданное составное условие и проверкой его истинности. Например для слова ГОРЕ проверка дает: Ø(1®(1Ú1)) = Ø(1®1) = Ø1 =0.

Дата добавления: 2014-01-20