Автономного риска

СТАТИСТИЧЕСКИЕ МЕТОДЫ ОЦЕНКИ

Вопрос

Статистические риски должны соответствовать трем основным требованиям:

1. Эти риски должны количественно измеряться;

2. Риск должен быть однородным, то есть относиться к большой массе одних и тех же событий;

3. Требование нейтральности единичного события к общей совокупности происходящих событий, то есть ущерб от единичного события должен быть ничтожно малым по сравнению с общей суммой убытков от всего множества событий происшедших одновременно.

Пример 1: крупная строительная фирма строит поселок из одноэтажных домов.

Пример 2: небольшая фирма взяла подряд на строительство коттеджа на одну семью.

В каком случае для строителей риски будут статистические, а в каком нет и почему?

Для крупных фирм инвестиционные риски как правило статистические. Для малых фирм не выполняется обычно третье требование – незначимость единичного события по отношению к общей массе происходящих событий. Малая фирма из-за недостатков ресурсов не может диверсифицировать свои риски, т.е. сделать нестатистические риски статистическими.

Строгие статистические методы оценки и учета риска:

1. Риск оценивается по коэффициенту вариации годовых чистых денежных поступлений.

;

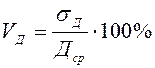V_Д – коэффициент вариации чистых денежных поступлений;

σ_Д - среднее квадратичное отклонение величины D от среднего значения (размах отклонений);

Д _ср – среднее значение годовых чистых денежных поступлений.

Чем больше коэффициент вариации, V_Д тем риски будут больше.

2. Риск оценивается по вероятности превращения ЧДД в ноль.

I – интервал изменения значений ЧДД. Заштрихованная площадь под кривой нормального распределения эквивалентна вероятности Р_А и Р_Б превращения ЧДД проектов А и Б в ноль.

Вероятность того, что ЧДД будет нулевым больше у проекта Б, т.к. дисперсия средней у этого проекта больше.

Снизить риски в общем случае можно следующим образом:

- создавать резервы денежных средств под непредвиденный случай;

- риски могут быть застрахованы в специальных фирмах;

- снизить величину риска можно посредством его дальнейшей диверсификации, т.е. распределения.

Оценка риска по коэффициенту вариации годовых чистых

денежных потоков

Коэффициент вариации годовых чистых денежных поступлений:

;

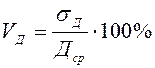Среднеквадратическое отклонение:

;

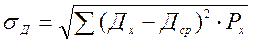Среднее значение годовых чистых денежных поступлений:

;

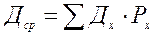х=1-n – количество вероятных исходов, или событий.

Пример: сделана оценка годовых чистых денежных потоков по двум проектам А и Б. Продолжительность реализации этих проектов – один год. Оценка сделана в тыс. руб.

Состояние	Проект А	Проект Б
Дх	Рх	Дх	Рх
Глубокий спад		0,1		0,1
Средний спад		0,2		0,2
Нормальное состояние		0,4		0,4
Небольшой подъем		0,2		0,2
Максимальный подъем		0,1		0,1

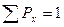
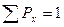
Решение:

Рассчитать коэффициент вариации величины Д и выбрать менее рискованный проект.

Из таблицы видно, что из двух проектов среднее значение Д одинаково Д=4000. В проекте Б разброс значений значительно больше, чем в А.

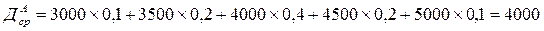
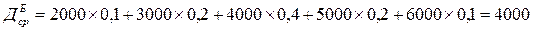
Рассчитаем среднеквадратическое отклонение чистых денежных потоков.

А: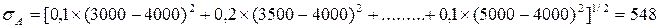

Б: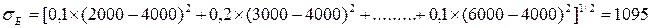

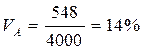
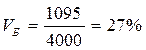
Проект Б более рискованный, т.к. коэффициент вариации больше. Таким образом, коэффициент вариации необходимо рассчитать по всем годам жизненного цикла.

Проблема в том, что риски изменяются во времени. На 2-ой, 3-ий и последующие годы проекта риски, как правило, будут увеличиваться с точки зрения точности прогноза.

В таблице, приведенной в примере, даны субъективные вероятности событий. Для определения субъективных вероятностных событий опрашивают группу экспертов, которые оценивают вероятности тех или иных событий. Затем эти значения усредняются и получают субъективные вероятности. Оценку субъективной вероятности можно получить и от неспециалиста в области экономической статистики.

Например, главный бухгалтер утверждает, что крупный дебитор вернет долг с вероятностью 0,6, а не вернет с вероятностью 0,2. Очевидно что эти значения нужно пронормировать на 1. Субъективная вероятность возврата долга Р₁=0,6/(0,6+0,2)=0,75. Субъективная вероятность того, что долг не будет возвращен: Р₂=0,2/(0,6+0,2)=0,25.

Оценка риска по вероятности превращения

ЧДД в нулевое значение.

Пример оценки того, что ЧДД может принимать нулевое или отрицательное значение.

По проекту было рассчитано среднеквадратическое отклонение:

σ_ЧДД=444 тыс.руб. и среднее значение ЧДД_ср=116 тыс.руб. Определить вероятность того, что ЧДД будет отрицательным и проект окажется неэффективным.

Решение:

Определим на каком расстоянии ЧДД_ср находится от нулевой отметки при условии, что расстояние измеряется в среднеквадратических отклонениях.

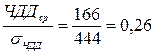стандартных отклонений

Фрагмент таблицы нормального распределения.

Число стандартных отклонений	Вероятность отклонений от средней, Р
0,2 0,25 0,26 0,3	0,42 0,4 0,39 0,38

Видно, что 0,26 стандартных отклонений соответствуют вероятности Р=0,39. Вероятность того, что ЧДД 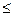0 равна Р=0,39, тогда вероятность, что ЧДД > 0 будет равна Р=0,59.

Принятие окончательного решения по реализации проекта зависит от субъективного восприятия риска инвестором. Если он считает, что вероятность (0,59) того, что ЧДД будет положительным достаточна, то проект будет реализован.

Дата добавления: 2014-01-20