Свойства средней арифметической

На основе исходных данных вначале подсчитываются средние величины, а затем находятся отклонения от средних. Рекомендуется в расчетах показателей вариации пользоваться формулой средней взвешенной.

Однородная статистическая совокупность – это такая совокупность, для которой различия между индивидуальными значениями признака не очень значительны, т.е. мало отличаются от среднего.

Основной количественной характеристикой степени однородности служит коэффициент вариации.

Обычно считается, что этот коэффициент в однородной статистической совокупности не превышает 33%.

Среди различных показателей вариации особое место принадлежит дисперсии, так как этот показатель обладает специальными свойствами, позволяющими упростить порядок его расчета.

2. Свойства средней арифметической и дисперсии

Показатели средняя арифметическая и дисперсия обладают некоторыми особыми свойствами, которые позволяют в ряде случаев упростить порядок их расчета для статистических совокупностей, обладающих большой численностью, но расчлененных на более малочисленные группы.

1) При увеличении или уменьшении всех частот отдельных значений признака в k раз значение средней арифметической не изменяется:

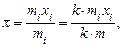
где k – любое натуральное число[2].

2) Если все индивидуальные значения признака умножить или разделить на некоторое число k, то и среднее значение увеличится или уменьшится в k раз:

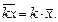
3) Средняя суммы или разности двух величин равна сумме или разности их средних:

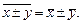
4) Если значение признака постоянно (т.е. равно некоторой константе С), то и средняя величина равна этой константе:

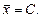
5) Сумма отклонений значений признака от средней арифметической равна нулю.

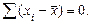
Дата добавления: 2014-01-20