Свойства дисперсии

1) Если значение признака постоянно (т.е. равно некоторой константе С), то дисперсия равна нулю.

2) Если все значения признака увеличить или уменьшить на постоянную величину, то дисперсия не изменится:

3) Если все значения признака уменьшить или увеличить в k раз, то дисперсия уменьшится или увеличится в k ² раз:

4) Если рассчитать средний квадрат отклонений от любой величины A, которая отличается от средней арифметической, то этот квадрат будет больше, чем дисперсия:

Если A ≠ , то

(свойство минимальности).

5) Правило сложения дисперсий:

Общая дисперсия статистической совокупности, разделенной на отдельные группы, равна сумме так называемой межгрупповой дисперсии (или дисперсии внутригрупповых средних) и средней из внутригрупповых дисперсий, или:

где 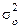– общая дисперсия;

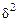– межгрупповая дисперсия;

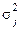– внутригрупповая дисперсия в j -той группе;

– средняя из внутригрупповых дисперсий.

Межгрупповая дисперсия рассчитывается следующим образом:

1) предположим, что мы выполнили группировку статистической совокупности, т.е. разделили ее на несколько групп;

2) затем в каждой группе мы вычисляем отдельно средние величины признака , которые называются «внутригрупповые средние»;

3) затем мы рассчитываем общую среднюю для всей совокупности.

Тогда межгрупповая дисперсия находится по формуле:

где 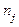– численность j -той группы (j = 1 …k);

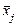– внутригрупповая средняя в j -той группе;

– общая средняя.

Средняя из внутригрупповых дисперсий равна следующей величине:

где 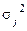– внутригрупповая дисперсия в j -той группе.

Более подробно расчет межгрупповой дисперсии и проверка правила сложения дисперсий изучается на практических занятиях.

3. Изучение структурных характеристик вариационного ряда

При изучении средних величин мы уже отмечали, что мода и медиана являются показателями, характеризующими структуру вариационного ряда, то есть распределение его частот. Как уже отмечалось, мода – это значение признака, наиболее часто встречающееся в данной совокупности. В дискретном ряду модой является просто значение с наибольшей частотой (или частостью).

В интервальном вариационном ряду мода рассчитывается по формуле:

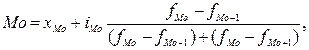
где

- нижняя граница модального интервала

- величина модального интервала

- частоты (или частости) соответственно модального, предшествующего и последующего интервала.

Модальный интервал – это соответственно интервал – имеющий наибольшую частоту (или частость).

Медиана – это условная величина, которая делит всю статистическую совокупность пополам. В дискретном ряду медиана находится как число, расположенное в середине упорядоченного вариационного ряда (если сумма частот является нечетным числом, то медиана совпадает со средним значением в данном ряду, а если – четным, то медиана рассчитывается как полусумма двух средних значений).

В интервальном ряду медиана определяется по формуле:

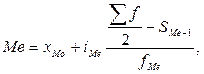
где

- нижняя граница медианного интервала

- величина медианного интервала

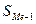- сумма накопленных частот (частостей) в интервале предшествующем медианному

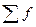- сумма частостей.

- порядковый номер медианы в ранжированном ряду.

По соотношению между модой, медианой и средней арифметической можно судить о симметричности ряда распределения.

Симметричным является распределение, в котором частоты двух вариантов, равноотстоящих от центра распределения в обе стороны, равны между собой. В таком распределении частот средняя арифметическая, мода и медиана равны между собой:

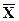= Me =Mo

Если средняя арифметическая превышает значение медианы и моды, то имеет место правосторонняя асимметрия, т.е. большая часть единиц изучаемой совокупности имеет значения, превышающие значение моды.

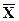> Me > Mo

Если, наоборот, средняя арифметическая меньше медианы и моды, то имеет место левосторонняя асимметрия, т.е. большая часть единиц изучаемой совокупности имеет значение признака ниже модального.

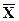< Me < Mo

Моду и медиану называют структурными средними, так как они дают количественную характеристику структуры распределения частот в вариационном ряду. К структурным характеристикам относятся и другие порядковые характеристики вариационного ряда: квартили, делящие ряд на четыре равных части, децили, делящие ряд на 10 равных частей, квинтили, делящие ряд на пять равных частей и другие.

Очевидно, что для деления ряда на четыре части, необходимо рассчитать три квартиля, причем второй квартиль совпадает по своему значению с медианой. Первый и третий квартиль, соответственно, рассчитывают по формулам:

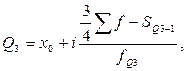
Децили нашли широкое применение в анализе степени дифференциации различных социально-экономических явлений.

Общая схема расчета децилей следующая:

1) Поскольку децили отсекают десятые части совокупности, по накопленным частотам определяем интервалы, куда попадают порядковые номера децилей: для первого дециля – это интервал, куда попадает вариант, отсекающий 10% совокупности с наименьшими значениями признака; для второй – 20% и т.д.;

2) рассчитываем величину децилей по формулам, аналогичным формуле для расчета медианы.

Например, первый и девятый дециль находятся по формулам:

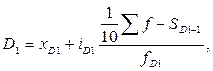
Лекция №6. Показатели анализа изменений структуры, концентрации и дифференциации признаков [3]

Дата добавления: 2014-01-20