Способы отбора единиц из генеральной совокупности

Значение выборочного метода состоит в том, что при минимальной численности обследуемых единиц проведение исследования осуществляется в более короткие сроки и с минимальными затратами труда и средств. Это повышает оперативность статистической информации, уменьшает ошибки регистрации.

Введение

Лекция №7. Методология организации выборочных наблюдений[5].

На данной лекции мы более подробно остановимся на способах расчета ошибок и численности выборки при проведении выборочных наблюдений. В этих формулах используются ранее изученные показатели вариации.

Основная цель любого несплошного наблюдения заключается в получении характеристик изучаемой статистической совокупности на основе обследования не всей совокупности, а некоторой ее части. Одним из наиболее распространенных видов несплошных наблюдений является выборочное наблюдение.

При выборочном методе наблюдения обследованию подвергается сравнительно небольшая часть всей изучаемой совокупности (обычно до 5–10%, реже до 15–25%). При этом изучаемая статистическая совокупность, из которой производится отбор части единиц, называется генеральной совокупностью. Отобранная из генеральной совокупности некоторая часть единиц, подвергающаяся обследованию, называется выборочной совокупностью, или просто выборкой.

Выборочное наблюдение проводится в целях распространения выводов, полученных по данным выборки, на генеральную совокупность.

В отличие от других видов статистических наблюдений, для выборочного наблюдения характерны особые, основанные на законах математической статистики, способы формирования выборочной совокупности.

1. Задачи выборочного наблюдения и различные способы формирования выборки

Задачами выборочного наблюдения являются:

P определение величины возможных отклонений показателей генеральной совокупности (средней или доли) от показателей выборочной совокупности;

P определение объема (численности) выборки, при котором пределы возможной ошибки не превысят некоторой, наперед заданной величины;

P определение вероятности того, что в проведенном выборочном наблюдении ошибка будет иметь заданный предел.

При некоторых исследованиях выборочный метод является единственно возможным, например, при контроле качества продукции (товара), если проверка сопровождается уничтожением или разложением на составные части обследуемых образцов.

При соблюдении правил научной организации обследования выборочный метод дает достаточно точные результаты, поэтому его целесообразно применять для проверки данных сплошного учета. Минимальная численность обследуемых единиц позволяет провести исследования более тщательно и квалифицированно. Например, при переписях населения практикуются выборочные контрольные обходы для проверки правильности записей сплошного наблюдения.

Особую актуальность приобрел выборочный метод в современных условиях перехода к рыночной экономике в связи с отказом от сплошной статистической отчетности. Изменения в характере экономических отношений повлияли на изменение функций учета и статистики, сокращение и упрощение отчетности. Возросли требования к управлению деятельностью предприятий (которые стали полностью самостоятельными хозяйствующими субъектами), а это в свою очередь усилило потребность в обеспечении надежной информацией, увеличило значение дальнейшего повышения ее оперативности. Все это обуславливает все более широкое применение выборочного метода в статистике.

По сравнению с другими методами сбора информации, основанными на несплошном наблюдении, выборочный метод имеет важную особенность. В основе отбора единиц для обследования положены принципы равных возможностей (вероятностей) попадания в выборку каждой единицы генеральной совокупности. Именно в результате соблюдения этих принципов исключается образование выборочной совокупности только за счет лучших или худших образцов. Это предупреждает появление систематических (тенденциозных) ошибок и делает возможным производить количественную оценку ошибки представительства (репрезентативности) отдельных единиц.

Поскольку изучаемая статистическая совокупность состоит из единиц с варьирующими (изменяющимися) признаками, то состав выборочной совокупности может в той или иной мере отличаться от состава генеральной совокупности. Это объективно возникающее расхождение между характеристиками выборки и генеральной совокупности представляет собой ошибку выборки. Она зависит от ряда факторов: степени вариации изучаемого признака, численности выборки, метода отбора единиц в выборочную совокупность, принятого уровня достоверности результата исследования.

Способыопределенияошибки выборки при различных приемах формирования выборочных совокупностей и распространения характеристик выборки на генеральную совокупность составляют основное содержание статистической методологии выборочного метода.

Проведение исследования социально-экономических явлений выборочным методом складывается из ряда последовательных этапов:

1) обоснование (в соответствии с задачами исследования) целесообразности применения выборочного метода;

2) составление программы проведения статистического исследования выборочным методом;

3) решение организационных вопросов сбора и обработки исходной информации;

4) установление доли выборки, т.е. части подлежащих обследованию единиц генеральной совокупности;

5) обоснование способов формирования выборочной совокупности;

6) осуществление отбора единиц из генеральной совокупности для их обследования;

7) фиксация в отобранных единицах (пробах) изучаемых признаков;

8) статистическая обработка полученной выборочной информации с определением обобщающих характеристик изучаемых признаков;

9) определение количественной оценки ошибки выборки;

10) распространение обобщающих выборочных характеристик на генеральную совокупность.

Применяя выборочный метод в статистике,обычно используют два основных вида обобщающих показателей: относительную величину (или долю) альтернативного признака [6] и среднюю величину количественного признака.

Относительная величина альтернативного признака характеризует долю (удельный вес) единиц в статистической совокупности, которые отличаются от всех других единиц этой совокупности только наличием изучаемого признака. Например, доля нестандартных изделий во всей партии товара, удельный вес продукции собственного производства в товарообороте предприятия общественного питания, удельный вес продавцов в общей численности работников магазина и т.д.

Средняя величина количественного признака – это обобщающая характеристика варьирующего признака, который имеет различные значения у отдельных единиц статистической совокупности. Например, средний образец в товароведении, средняя выработка одного продавца, средняя заработная плата одного работника магазина и т.д.

В генеральной совокупности доля единиц, обладающих изучаемым признаком, называется генеральной долей (обозначается р), а средняя величина изучаемого варьирующего признака – генеральной средней (обычно обозначается χ). В выборочной совокупности долю изучаемого признака называют выборочной долей, или частостью (обозначается w), а среднюю величину в выборке – выборочной средней (обозначается

Основная задача выборочного обследования в статистике состоит в том, чтобы на основе характеристик выборочной совокупности (частоты или средней получить достоверные суждения о показателях доли р или средней х) в генеральной совокупности.

Практика применения выборочного метода в экономико-статистических исследованиях использует следующие способы отбора единиц из генеральной совокупности:

индивидуальный отбор – в выборку выбираются отдельные единицы;

групповой отбор – в выборку попадают качественно однородные группы или серии изучаемых единиц;

комбинированный отбор как комбинация индивидуального и группового отбора.

Способы отбора определяются правилами формирования выборочной совокупности. При этом выборка может быть:

P собственно случайная;

P механическая;

P типическая, серийная;

P комбинированная.

Собственно случайная выборка состоит в том, что выборочная случайность образуется в результате случайного (непреднамеренного) отбора отдельных единиц из генеральной совокупности. При этом количество отобранных в выборочную совокупность единиц обычно определяется исходя из принятой доли выборки.

Доля выборки (или выборочная доля) есть отношение числа единиц в выборке n к числу единиц в генеральной совокупности N, т.е. n/N.

Механическая выборка состоит в том, что отбор единиц в выборочную совокупность производится из генеральной совокупности, разбитой на равные интервалы (группы). При этом размер интервала в генеральной совокупности равен обратной величине доли выборки. Так, при 2%-ной выборке отбирается каждая 50-я единица (1: 0,02), при 5%-ной выборке – каждая 20-я единица (1: 0,05) и т.д.

Таким образом, в соответствии с принятой долей отбора генеральной совокупности как бы механически разбивается на равновеликие группы. Из каждой такой группы в выборку отбирается лишь одна единица.

Для обеспечения репрезентативности (представительности) механической выборки все единицы генеральной совокупности должны располагаться в определенном порядке. При этом по отношению к изучаемому показателю единицы генеральной совокупности могут быть упорядочены по существенному, второстепенному или нейтральному признаку. Это важно для установления порядка отбора единиц в выборку.

Величина средней ошибки механической выборки теоретически должна определяться с учетом показателей внутригрупповых дисперсий. Но так как при механической выборке каждая группа представлена лишь одной единицей, то получить значения внутригрупповых дисперсий выборки практически невозможно. Поэтому для определения средней ошибки механической выборки используют формулы собственно случайной выборки.

В статистике довольно часто применяется так называемая типическая выборка.

При типической выборке генеральная совокупность вначале расчленяется на однородные типические группы, а затем с помощью собственно-случайной или механической выборки производится индивидуальный отбор единиц в выборочную совокупность.

Важной особенностью типической выборки является то, что она дает более точные результаты по сравнению с другими способами отбора единиц в выборочную совокупность. Репрезентативность типической выборки обеспечивается расчленением генеральной совокупности на качественно однородные группы. Это обусловливает представительство в выборке каждой типической группы.

При определении ошибки типической выборки в качестве показателя вариации выступает средняя из внутригрупповых дисперсий.

Довольно широко в статистике применяется так называемая серийная, или гнездовая выборка.

При серийной выборке из генеральной совокупности отбираются не отдельные единицы, а целые их серии (гнезда). Внутри же каждой из попавшей в выборку серии обследуются все без исключения единицы, т.е. применяется сплошное наблюдение.

Отбор отдельных серий в выборочную совокупность осуществляется либо посредством собственно случайной выборки, либо механическим отбором. Практически серийная выборка производится, как правило, по схеме бесповторного отбора.

По сравнению с типической выборкой серийная выборка дает более высокую ошибку репрезентативности. Это обусловлено тем, что при серийной выборке, как, правило, обследуется сравнительно небольшое число серий.

Рассмотренные способы выборки на практике обычно применяются не в «чистом» виде, а комбинируются в различных сочетаниях и с различной последовательностью.

При одноступенчатом способе отбора каждая отобранная единица подвергается изучению по заданному признаку. Так обстоит дело при собственно-случайной выборке.

При многоступенчатом способе отбора производят отбор из генеральной совокупности отдельных групп, а из групп выбираются отдельные единицы. Так производится типическая выборка с механическим способом отбора единиц выборочную совокупность.

Комбинированная выборка может быть двухступенчатой. При этом генеральная совокупность сначала разбивается на группы. Затем производят отбор групп, а внутри последних осуществляется отбор отдельных единиц.

2. Понятие «ошибка выборки» и способы ее расчета

Теоретической основой выборочного метода является теорема Чебышева (или «Закон больших чисел»), которая применительно к выборке может быть записана в следующем виде:

P { | χ – 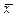| < t μ} → 1, (7.1)

где χ – средняя величина признака для генеральной совокупности;

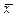– средняя величина признака для выборочной совокупности;

P – вероятность того, что разность между выборочной средней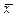и генеральной средней χ будет меньше, чем t μ;

t μ = Δ – так называемая предельная вероятная ошибка выборки;

μ – средняя стандартная ошибка выборки;

t – так называемый коэффициент доверия, связывающий размер ошибки и вероятность ее возникновения. Величина t находится по таблице значений функции Лапласа (такая таблица обычно приводится в качестве приложения к многим учебникам по математической статистике и теории вероятностей).

Наиболее часто используемые в экономике уровни вероятности Р и соответствующие им значения t для выборок достаточно большого объема (n > 30) приведены в табл. 7.1.

Таблица 7.1

Дата добавления: 2014-01-20