Формулы для расчета средней стандартной ошибки выборки

Табличные значения функции Лапласа

T	1,0	1,96	2,0	2,58	3,0
P	0,683	0,950	0,954	0,99	0,997

Средняя (стандартная) ошибка выборки (μ) характеризует среднюю величину возможных расхождений выборочной и генеральной средней (или доли). Ее значение зависит от определяемой характеристики (средней или доли), способа отбора (повторный или бесповторный) и вида выборочного наблюдения (случайный, механический, типичный, серийный, комбинированный).

Для организации выборочного наблюдения экономических явлений наиболее часто используют формулы, представленные в табл. 7.2.

Таблица 7.2

Способ отбора	Ошибка μ для средней	Ошибка μ для доли
Собственно случайный, повторный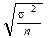
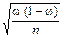
Случайный и механический, бесповторный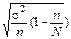
Типический, бесповторный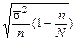
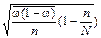
Серийный, бесповторный, с равновеликими сериями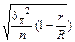

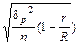
В табл. 7.2 приняты следующие обозначения:

σ² – дисперсия средней в выборочной совокупности;

ω – доля признака в выборочной совокупности (частость);

n – число единиц в выборочной совокупности;

N – число единиц в генеральной совокупности;

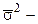средняя из выборочных дисперсий типических групп;

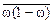– средняя из произведений частостей на их дополнение до единицы;

R – число серий в генеральной совокупности;

r – число серий в выборочной совокупности;

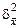– межгрупповая (или межсерийная) дисперсия средних;

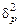– межгрупповая (или межсерийная) дисперсия долей.

Исходя из формулы (7.1), можно вывести формулу для определения границ изменения генеральной средней χ (если известна выборочная средняя 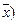при заданной вероятности P:

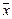– t μ ≤ χ ≤ 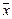+ t μ,(7.2)

а также формулу для определения границ изменения доли признака d в генеральной совокупности, если (известна выборочная доля ω)при заданной вероятности P:

ω – t μ ≤ d ≤ ω + t μ.(7.3)

В формулах (7.2) и (7.3) вначале для заданного значения вероятности P по таблице определяется значение коэффициента доверия t, затем рассчитываются значения ошибки μи рассчитывается предельная ошибка Δ = t μ.

3. Расчет оптимальной численности выборки

Определение необходимой численности выборки при заданной величине допустимой (предельной) ошибки выборки основывается на формуле Δ = t μ и формулах для определения ошибкиμ, приведенных в табл. 7.2. Так как генеральная дисперсия неизвестна, то используют какие-либо ее оценки. Формулы для определения достаточной (оптимальной) численности выборки представлены в табл. 7.3.

Значение вероятности P достижения заданного предела ошибки выборки Δ определяется по таблице значений функции Лапласа, исходя из соотношения:

,

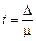т.е. вначале рассчитывается t, а затем по таблице определяется P.

Таблица 7.3

Дата добавления: 2014-01-20