Введение. Лекция №10. Построение уравнений тренда и уравнений парной линейной регрессии

Лекция №10. Построение уравнений тренда и уравнений парной линейной регрессии

На предыдущей лекции мы говорили о сглаживании динамических рядов и о том, что аналитическое сглаживание осуществляется на основе так называемых уравнений тренда. А перед этим, изучая методы анализа статистических взаимосвязей, мы говорили о построении так называемых уравнений регрессии. На самом деле между уравнениями тренда и уравнениями регрессии имеется немало общего и для расчета их параметров используется один и тот же метод наименьших квадратов (МНК). Разница лишь в том, что уравнения тренда выражают зависимость некоторого показателя от времени, а уравнения регрессии – статистическую зависимость между двумя и более показателями. На данной лекции мы будем более подробно изучать построение этих уравнений с помощью разработанного в математической статистике метода (МНК). И прежде всего кратко рассмотрим сущность этого метода.

1. Сущность метода наименьших квадратов

Этот метод более подробно изучается в математической статистике и в эконометрике.

Его сущность заключается в том, что параметры аналитической функции, используемой для сглаживания ряда, подбираются таким образом, чтобы минимизировать сумму квадратов отклонений расчетных (теоретических) значений динамического ряда от фактических (исходных) значений. То есть находится:

,

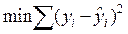где 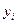- фактические значения показателя (исходные статистические данные), а 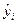- расчетные значения (полученные на основе построенного уравнения тренда или регрессии). Например, для уравнения линейного тренда такая сумма квадратов имеет вид:

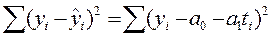
Так как значения 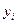и 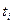нам известны, то сумма квадратов в действительности является функцией многих переменных, в качестве которых выступают неизвестные значения параметров уравнений тренда (или регрессии).

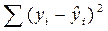= Q (a ₀, a ₁, a ₂,… a_n)

Таким образом, задача поиска параметров функций, сглаживающих исходный ряд, преобразуется в задачу поиска min Q (a ₀, a ₁, a ₂,… a_n).

Как известно из высшей математики, задача поиска экстремума (минимума или максимума) некоторой функции обычно решается путем ее дифференцирования и приравнивания частных производных к нулю.

Точно так же данная задача решается и в этом случае. Находятся частные производные функции Q (a ₀, a ₁, a ₂,… a_n) по каждому из параметров и приравниваются к нулю. Получается система уравнений, в которой число неизвестных и параметров совпадает с числом параметров, которые необходимо найти. Эта система в статистике называется системой «нормальных уравнений». В зависимости от вида конкретного уравнения тренда или регрессии эти системы имеют разный вид.

2. Построение уравнений регрессии

Дата добавления: 2014-01-20