Расчет параметров парной линейной регрессии

Исходные данные	Вспомогательные расчеты
x	y	x^2	x × y	ŷ = f (x)
…
Σ

Система нормальных уравнений для поиска параметров двухфакторной линейной регрессии (y = a ₀ + a ₁ x ₁ + a ₂ x ₂) имеет более сложный вид, чем система (10.1):

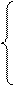Σ y = na ₀ + a ₁ Σ x ₁ + a ₂Σ x ₂;

Σ yx ₁= a ₀ Σ x ₁ + a ₁ Σ x ₁² + a ₂ Σ x ₁ x ₂; (10.3)

Σ yx ₂= a ₀ Σ x ₂ + a ₁ Σ x ₁ + a ₂ Σ x ₂²;

Очень похожий вид имеет система нормальных уравнений для расчета параметров квадратической регрессии (y = a ₀ + a ₁ x + a ₂ x ²):

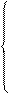Σ y = na ₀ + a ₁ Σ x + a ₂Σ x ²;

Σ yx ₁ = a ₀ Σ x + a ₁ Σ x ² + a ₂ Σ x ³; (10.4)

Σ yx ₂ = a ₀ Σ x ² + a ₁ Σ x ³ + a ₂ Σ x ⁴;

Система (10.4) получается из системы (10.3) и наоборот путем простейшей замены переменных x ₁ = x; x ₂ = x ².

Эти системы также решаются методом определителей.

Вначале находится определитель Δ матрицы коэффициентов при неизвестных, затем столбцы этой матрицы поочередно заменяются столбцом свободных членов системы нормальных уравнений, и рассчитываются еще три соответствующих определителя: Δ₀, Δ₁, Δ₂.

Параметры a₀ , a₁, a₂ рассчитываются по формулам:

a₀= Δ₀/ Δ; a₁ = Δ₁/ Δ; a₂ = Δ₂/ Δ

Подробнее различные сложности, которые возникают при построении уравнений нелинейной и множественной регрессии, мы рассмотрим на следующей лекции.

3. Построение уравнений тренда

Для расчета параметров уравнений тренда также используется метод наименьших квадратов (МНК), но при этом используется особый прием – введение условного обозначения времени. За счет введения условного обозначения времени существенно упрощаются формулы для расчетов параметров уравнений тренда. В теории статистики доказывается, что результат расчета параметров не зависит от изменения начала координат на оси отсчета периодов времени. Это связано с тем, что время изменяется равномерно и в одном направлении. Расчет параметров уравнений регрессии значительно сложнее именно из-за того, что ввести условное обозначение переменной x в данном случае не удается.

При расчете параметров уравнений тренда обычно строится вспомогательная таблица, в которой специально вводят условное обозначение времени.

Условное время вводят таким образом, чтобы Σ t = 0. Если число реальных периодов (моментов) времени нечетное, в середине ставится 0, а затем отсчет ведется вправо и влево от нуля (как считают в истории «годы до нашей эры»). Если число периодов четное, то 0 пропускается; при этом отсчет вправо ведется от 1, отсчет влево – от –1.

Пример условного обозначения времени показан в табл. 10.1. Если заменить в ранее приведенных системах нормальных уравнений (10.1) и (10.4) переменную x на переменную t и заменить в полученных системах 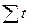и 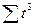на ноль, получим следующие, более простые системы:

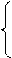na ₀ = Σy;

a₁Σx² = Σxy. (10.5)

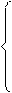Σ y = na ₀ + a ₂Σ t ²;

Σyt = a₁ Σt²; (10.6)

Σ yt² = a₀ Σt² + a₂ Σt⁴;

Решая системы (10.5) и (10.6), получаем простейшие формулы для расчета параметров соответственно линейного (10.7) и квадратического тренда (10.8).

Таблица 10.2

Вспомогательная таблица для расчета параметров уравнений линейного и квадратического тренда

Период реаль-ного времени	Условное обозначение времени	yxt	y xt^2	y xt^4
Условное t	Условное t ^2	Условное t ^4
	–2
	–1
Сумма:

Формулы для расчета параметров тренда будут иметь следующий вид:

а) для линейного тренда (y = a ₀ + a ₁ t):

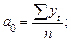
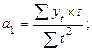(10.7)

б) для уравнения квадратического тренда, т.е. параболы

(y = a ₀ + a ₁ t + a ₂ t ²):

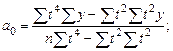
(10.8)

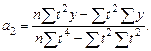
Необходимо обратить внимание, что параметр a ₁ рассчитывается по такой же формуле, как и для линейного тренда.

Обычно при построении уравнений тренда или регрессии возникает проблема выбора такой математической формы зависимости, которое лучше сглаживает исходный ряд данных.

Для этого используют различные способы, в том числе графический анлиз, или, как уже отмечалось, рассчитывается ошибка аппроксимации и выбирается то из уравнений, для которого эта ошибка меньше. Помимо ошибки аппроксимации, существуют и другие критерии оценки надежности построенных уравнений и отбора тех, которые наиболее адекватно описывают реальную статистическую зависимость. Более подробно эти критерии изучают в курсе эконометрики. В частности, можно рассчитать корреляционное отношение или индекс детерминации (квадрат корреляционного отношения) и оценивать, насколько эти показатели близки к 1.

4. Расчет корреляционного отношения на основе уравнения регрессии

Корреляционное отношение является одним из показателей тесноты связи, которая рассчитывается для оценки степени тесноты связи, если зависимость между двумя показателями не является линейной (т.е. линейный коэффициент корреляции может не показать наличие связи).

Для расчета корреляционного отношения необходимо вначале построить уравнение парной регрессии, выражающее зависимость между показателями x и y.

Пусть y = f (х) – уравнение парной регрессии.

Если уже рассчитаны его параметры, необходимо рассчитать все теоретические (или расчетные) значения показателя y – так же, как это делается при расчете ошибки аппроксимации.

Затем корреляционное отношение рассчитывается по фор­муле:

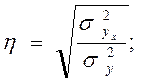
где 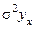– дисперсия теоретических значений y;

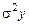– дисперсия фактических значений y.

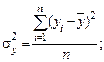
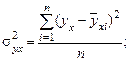
В этой формуле 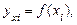где f (х) – построенное уравнение регрессии.

Для расчета корреляционного отношения η строится обычно вспомогательная таблица следующего вида (табл.10.3):

Таблица 10.3

Вспомогательная таблица для расчета корреляционного отношения

	y	yх	yх – ух	(yх – yх) ^2
х 1	y 1	f (х)
х 2	y 2	f (x)
х 3	y 3	f (x)
.	.
хn	yn	f (x)
	Σ	Σ	Σ	Σ

Корреляционное отношение обладает свойством: 0 ≤ η ≤ 1.

Чем ближе η к 1, тем связь более тесная. Для оценки степени тесноты связи с помощью корреляционного отношения используется специальная шкала, которую называют шкалой Чеддока (по имени автора, предложившего данную шкалу).

Дата добавления: 2014-01-20