Исходные данные для построения уравнений регрессии

Пример

Предположим, что нам необходимо использовать зависимость расходов семьи на покупку товаров длительного пользования от различных факторов и для этого по исходным данным, приведенным в таблице 11.1, построить уравнение двухфакторной линейной регрессии. Предварительно необходимо отобрать из всех возможных факторных признаков, по которым имеются исходные данные, два фактора, между которыми нет корреляционной зависимости, и в то же время связь каждого из них с результативным показателем y сильнее, чем их связь между собой.

Таблица 11.1

№№	x1	x2	x3	x4	x5	y
						0,8
				5,3
				4,7
				3,3		0,5
				3,75		2,5
				3,2		1,5
Σ				49,3		27,3

В таблице 11.2 используются следующие обозначения:

Обозначения факторных признаков:

x₁- число членов семьи,

x₂ - доход семьи,

x₃ - число детей в семье,

x₄ - среднедушевой доход,

x₅ - затраты на питание,

y - расходы на покупку товаров длительного пользования.

Прежде чем строить уравнения регрессии, необходимо выполнить анализ мультиколлинеарности исходных переменных, чтобы отобрать те факторы, которые целесообразно включить в соответствующие уравнения (модели).

С этой целью рассчитаем коэффициенты парной корреляции между каждой парой факторов и отберем те факторы, коэффициент корреляции между которыми удовлетворяет условиям:

1) r (x_i,x_j)< 0,8, и одновременно при этом:

2) r (x_i,x_j)£ r (x_i,y)

3) r (x_i,x_j) £ r(x_j,y)

Для расчета каждого коэффициента парной корреляции построим вспомогательную таблицу следующего вида (на примере расчета коэффициента корреляции между факторами x₁ и x₄):

Таблица 11.2.

Вспомогательная таблица для расчета парного линейного коэффициента корреляции между факторами x₁ и x₄

Исходные данные	Вспомогательные расчеты
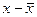
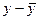
№/№	x1	x4		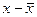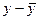	()^2	()^2	()()
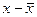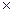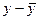			-1,80	-1,73	3,24	2,99	3,11
			-0,80	2,27	0,64	5,15	-1,82
			-0,80	3,27	0,64	10,69	-2,62
		0,8	-0,80	-1,93	0,64	3,72	1,54
			0,20	0,27	0,04	0,07	0,05
			0,20	0,27	0,04	0,07	0,05
			0,20	1,27	0,04	1,61	0,25
		0,5	0,20	-2,23	0,04	4,97	-0,45
		2,5	1,20	-0,23	1,44	0,05	-0,28
		1,5	2,20	-1,23	4,84	1,51	-2,71
Σ		27,3		0,00	11,6	30,86	-2,84

Средние значения признаков находим по формулам:

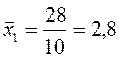
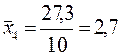
После подсчета сумм в нижней строке таблицы, находим линейный коэффициент корреляции:

r (x₁ , x₄) =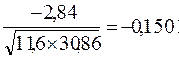

Аналогично рассчитаем коэффициенты парной корреляции между всеми остальными факторами и запишем их значения в виде матрицы:

Таблица 11.3

Дата добавления: 2014-01-20