Количественные показатели надежности невосстанавливаемых систем

ТЕМА 2. РАСЧЕТ НАДЕЖНОСТИ НЕВОССТАНАВЛИВАЕМЫХ СИСТЕМ.

Показатели надежности – это количественные характеристики одного или нескольких частных свойств, определяющих надежность объекта.

Для невосстанавливаемых систем основным свойством, определяющим их надежность, является безотказность. Так как отказы являются случайными событиями, то все показатели надежности, в том числе и безотказность, являются вероятностными характеристиками. Основной случайной величиной в теории надежности принято рассматривать наработку объекта до отказа.

Наработкой до отказа называется продолжительность или объем работы объекта от начала его эксплуатации и до возникновения первого отказа, измеряемое в часах, циклах работы, количестве переключений, в километрах и других величинах.

Для электронных систем основной случайной величиной является время τ, которое определяет время безотказной работы объекта, определяемое от момента его включения в работу и до появления первого отказа.

Рассмотрим количественные показатели безотказности для невосстанавливаемых систем.

1. Р(t) – вероятность безотказной работы в интервале времени (0, t).

Математически она определяется по следующей формуле:

Р(t)=Р(τ > t), (1)

То есть Р(t) – это вероятность того, чтослучайная величина τ будет больше требуемого времени t.

В качестве времени t используется, например, гарантийный срок эксплуатации объекта. Время t может характеризовать произвольное значение времени, для которого определяется характеристика Р(t).

Статистически вероятность Р(t)= Р^*(t) определяется по результатам испытаний следующим образом:

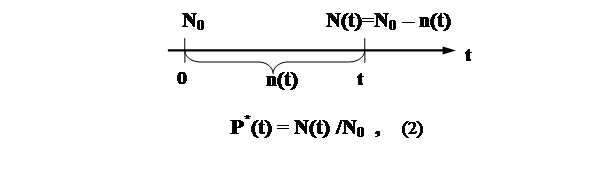
где N₀ – общее число однотипных объектов, поставленных на испытание (например, генераторов, осциллографов);

n(t) – число отказавших объектов за время испытания t;

N(t) - число неотказавших объектов за время t.

Свойства вероятности безотказной работы:

1) 0 ≤ P(t) ≤ 1;

2) если t₂ > t₁ , то P(t₁) > P(t₂); т.е.P(t) – функция убывающая;

3) при t=0 P(t=0)=1, т.е. в момент включения объекта он принимается абсолютно надежным;

4) при t=∞ P(t=∞)=0, т.е. объект обязательно откажет.

2. Q(t) – вероятность отказа объекта за время t.

Математически она определяется по следующей формуле:

Q(t) = P(τ < t), (3).

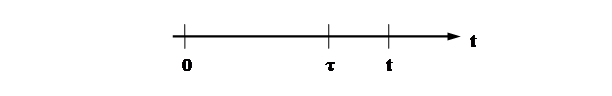
Из (3) следует, что Q(t) представляет собой интегральную функцию (закон) распределения случайной величины τ.

Статистически величина Q(t) = Q^*(t) определяется по формуле:

,

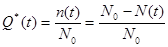т.е. это отношение числа отказавших объектов n(t) за время испытания t к общему числу объектов, поставленных на испытание.

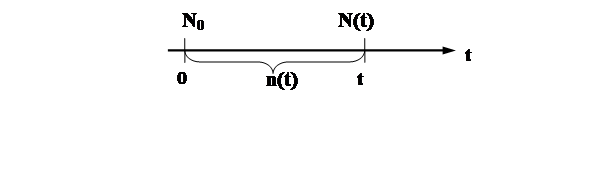
Отказ объекта и безотказная работа представляют собой полную группу несовместных событий. Поэтому сумма вероятностей P(t) и Q(t) равна единице, т. е.

P(t) + Q(t) =1

3. ƒ(t) – дифференциальная функция распределения случайной величины τ.

Эту характеристику еще называют так: плотность распределения отказов, плотность вероятности отказов, дифференциальный закон распределения отказов.

Дифференциальная функция распределения отказов ƒ(t) математически представляет собой производную от интегральной функции распределения отказов:

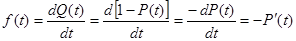, (4)

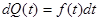, (5)

Проинтегрируем обе части равенства (5):

;

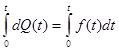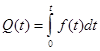, (6)

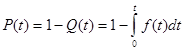, (7).

Статистическое значение ƒ(t) определяется по формуле:

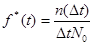(1/час), (8).

Назначается основной интервал времени для испытания (0, t) и затем дополнительный Δt (от t до t+Δt).

За время t отказывает n(t) объектов; N(t)=N₀ - n(t) – число неотказавших объектов за время t; n(Δt) – число отказавших объектов за время Δt; N(t + Δt) – число неотказавших объектов за время (0 ÷ t+ Δt); N(t)≥N(t+Δt).

ƒ^*(t) – это отношение числа отказавших объектов n(Δt) на интервале Δt в единицу времени к общему числу объектов N₀ , поставленных на испытание.

4. λ(t) – интенсивность отказов объектов.

Эта характеристика является основной характеристикой надежности для элементов, входящих в состав любого устройства, прибора, системы. Без нее рассчитать показатели надежности невозможно.

Интенсивность отказа, определяемая по результатам испытаний находится по формуле:

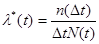, (9).

λ^*(t) – это отношение числа отказавших объектов за время Δt в единицу времени к числу объектов неотказавших за время t (от 0 до t).

Выведем аналитическое выражение для интенсивности отказов элемента. Для этого рассмотрим такую задачу:

Пусть объект проработал безотказно на интервале времени от 0 до t. Необходимо определить вероятность отказа объекта на следующем интервале времени Δt (от t до t+Δt).

Обозначим: А – событие, состоящее в безотказной работе объекта на интервале времени (0 ÷ t);

В – событие, состоящее в безотказной работе объекта на интервале времени Δt.

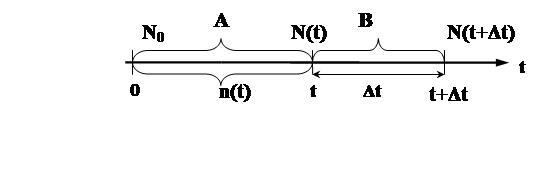
События А и В являются зависимыми. В соответствии с теоремой умножения зависимых событий можно записать:

Р(АВ) = Р(А) Р(В/А)=Р(В) Р(А/В), (1)

где Р(АВ) – вероятность безотказной работы объекта на интервале времени (0, t+Δt). Поэтому Р(АВ) = Р(t+Δt);

Р(А) – вероятность безотказной работы объекта на интервале времени (0,t). Поэтому Р(А) = Р(t);

Р(В/А) – вероятность безотказной работы объекта на интервале времени (t, t +Δt). Поэтому Р(В/А) = Р(Δt) – вероятность безотказной работы объекта на интервале времени Δt.

Выражение (1) можно записать в следующем виде:

Р(t+Δt) = Р(t) Р(Δt), (2).

Из выражения (2) следует:

.

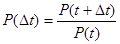Определим вероятность отказа объекта на интервале времени Δt:

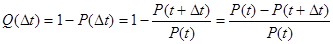. (3)

Разделим числитель и знаменатель уравнения (3) на Δt. Причем Δt→0.

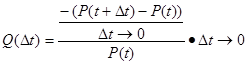, (4).

Числитель в выражении (4) определяет производную от вероятности безотказной работы Р(t). Поэтому:

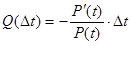(5)

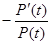- интенсивность отказа λ(t). Поэтому интенсивность отказа λ(t) определяется по формуле:

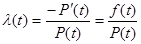(6).

Из этого выражения следует, что интенсивность отказа представляет собой условную плотность вероятности отказа в момент времени t при условии, что до этого момента t отказа объекта не произошло.

Из выражения (6) можно получить аналитическое выражение для статистического определения интенсивности отказа:

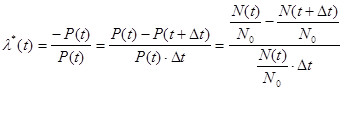(7)

Так как N(t) - N(t+Δt) = n(Δt), то

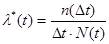(8).

Из выражения

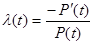(9)

можно получить соотношение, которое связывает интенсивность отказа λ(t) с вероятностью безотказной работы Р(t). Для этого умножим обе части уравнения (9) на dt и проинтегрируем их.

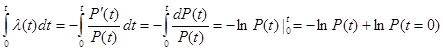
Итак: 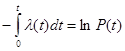(10).

В соответствии с определением логарифма выражение (10) запишем в виде:

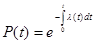(11)

λ(t) является важнейшей характеристикой для элементов любого устройства или системы. Если известны значения интенсивностей отказов для всех типов элементов, входящих в состав устройства (системы), то можно вычислить все показатели надежности этого устройства. Поэтому все разработчики элементной базы по результатам испытаний определяют интенсивности отказов для выпускаемых элементов и эти данные разработчики и эксплуатационники используют для оценки надежности устройств или систем. Результаты испытаний показали, что для любых типов элементов интенсивность отказа изменяется с течением времени по кривой, представляющей собой рисунок1.

λ (t)

Рисунок 1 – График функции λ(t).

I период – период приработки (выжигания) элементов, проводимый при заводских испытаниях. На нем интенсивность отказа λ(t) уменьшается из-за того, что отказавшие элементы заменяются. Этот период является достаточно коротким.

II период – период нормальной эксплуатации объекта. На нем интенсивность отказа является постоянной λ(t) = λ = const. Этот период (от t₁ до t₂) является достаточно длительным.

III период – период старения и износа элементов устройства. На нем интенсивность отказа резко возрастает, поэтому эксплуатировать изделие (объект) на этом периоде не рекомендуется.

Для периода приработки элемента можно использовать γ- распределение плотности вероятности отказа. На периоде II плотность вероятности отказов ƒ(t), а также вероятность отказа Р(t) имеют экспоненциальный закон распределения отказов. Покажем, что это так.

Подставим в выражение (11) значение λ(t) = λ, получим:

P(t) = e ^{–λ t} – убывающая экспонента.

Q(t) = 1-P(t) = 1- e ^{–λ t} – вероятность отказа на интервале II (возрастающая экспонента).

Плотность вероятности отказа:

ƒ(t) = -P^’(t) = - (e ^{–λ t})^’ = λ e ^{–λ t} – убывающая экспонента.

На периоде II законы надежности можно описывать математически с помощью двух законов распределения:

1) закон распределения Релея;

2) закон распределения Вейбулла.

Период нормальной эксплуатации является основным, поэтому в дальнейшем все показатели надежности мы будим оценивать для периода II.

5. Т₀ – средняя наработка до отказа.

Случайная величина τ является непрерывной величиной. Поэтому среднее значение этой величины будет определяться как математическое ожидание, то есть:

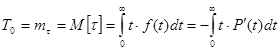(1)

Данный интеграл и(1) является не табличным. Поэтому приведем его к табличному виду: 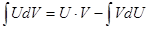. Итак:

.

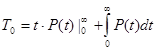Произведение tP(t) и его предел 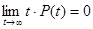, так как Р(t→∞) стремится к 0 быстрее, чем t→∞.

.

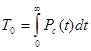Учитывая, что вероятность P(t) = e^-λ_c^t, получим:

.

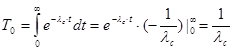Средняя наработка до отказа Т₀ для невосстанавливаемых нерезервированных систем равна величине, обратной интенсивности отказов системы.

Статистически по результатам испытаний величина Т₀ определяется по формуле:

,

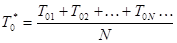где Т_0N – средняя наработка до отказа i-ого образца (i = 1÷N).

2. Понятие о структурных схемах надежности (ССН). Способы соединения элементов в ССН.

Под расчетом надежности понимают вычисление показателей надежности системы по известным вероятностным характеристикам элементов, входящих в состав системы, а также по известному виду соединений элементов с точки зрения их надежности и с учетом вида и способа используемого резервирования.

Каждому расчету надежности предшествует составление структурной схемы надежности (ССН), которая учитывает состав элементов и связи между ними. ССН составляется с использованием принципиальной или функциональной электрической схемы устройства или системы. При этом элементы любого типа обозначаются прямоугольником и нумеруются.

Все элементы в ССН имеют следующие способы соединения:

1) последовательное (используется при отсутствии резервирования в устройстве или системе);

2) параллельное (резервное);

3) смешанное (параллельно – последовательное).

Параллельное и смешанное используются в устройствах и системах с резервированием.

Рассмотрим показатели надежности для перечисленных способов соединения элементов.

При последовательном соединении элементов (рис. 1) отказ системы наступит тогда, когда откажет любой хотя бы один элемент, входящий в данную ССН.

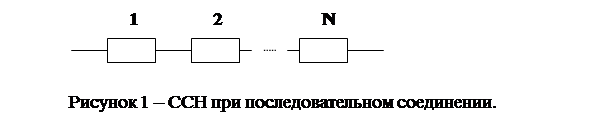
Вероятность безотказной работы:

Р_c(t) = P₁(t) · P₂(t) ·... · P_N(t) = e ^{– λ}₁ ^t · e ^{– λ}₂^t ·... · e ^{– λ}_N^t = e ^{– (∑ λ}_i^{) t} = e ^{– λ}_c^t,

где λ_с – интенсивность отказа системы.

При параллельном соединении элементов ССН имеет следующий вид (рис. 2):

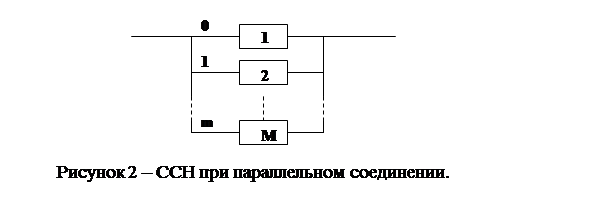
Здесь 0 – основной элемент первого типа;

1÷ m – резервные элементы соответствующих типов (могут быть того же типа как и основной).

Если вероятностные характеристики у основного и резервных элементов одинаковые, то схема будет иметь вид:

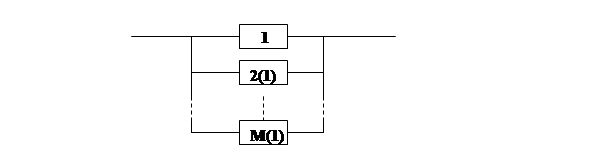
В такой системе или устройстве отказ наступит в том случае, если откажут все элементы: и основной, и резервные. Поэтому вероятность отказа системы будет определяться произведением вероятностей отказа элементов:

Q_c (t) = q₁(t) · q₂(t) ·... · q_m(t) = [1-p₁(t)] · [1-p₂(t)] ·... · [1-p_m(t)].

P_c(t) = 1 – Q_c(t).

При третьем способе соединения расчет надежности будет вычисляться следующим образом.:

1)ССН (рис. 3) разбивается на участки с однотипным соединением элементов;

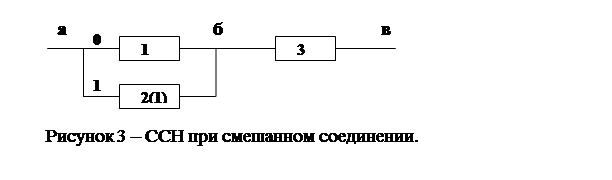
1) определяются вероятности безотказной работы каждого из участков;

2) определяется вероятность безотказной работы всей схемы по следующей формуле:

P_c(t) =P_аб(t) · P_бв(t);

3) определяется средняя наработка до отказа схемы по следующей формуле:

.

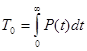3. Виды резервирования систем. Способы структурного резервирования.

Резервирование – это метод повышения надежности за счет введения избыточности определенного вида.

Различают следующие виды резервирования:

1) структурное – этот метод предусматривает использование избыточных структурных элементов. Резервироваться могут отдельные элементы, блоки и целые системы;

2) временное – предусматривает использование избыточного времени. Примеры:

- решение одной и той же задачи на ЭВМ дважды с последующим сравнением результатов решения;

- системы с повторением и накоплением сообщений в телемеханике;

3) информационное – предусматривает использование избыточной информации для повышения надежности (например: использование избыточных помехоустойчивых кодов).

Различают несколько способов структурного резервирования по следующим признакам:

1)по времени включения резервных объектов различают:

- постоянное резервирование.

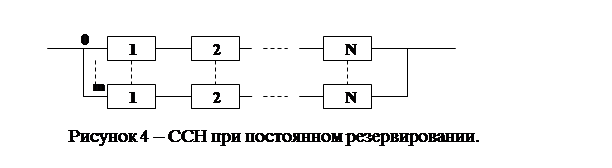
При этом способе резервирования и основная и резервная системы подключены к нагрузке постоянно и работают в одинаковом режиме;

- резервирование способом замещения:

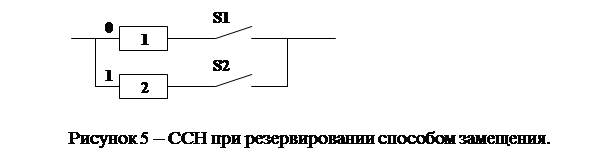
При этом способе под нагрузку включается сначала основной объект за счет включения элемента коммутации S1. При появлении отказа основного элемента в работу включается резервный элемент, а отказавший основной элемент отключается от нагрузки.

Управление работой элементов коммутации S1 и S2 осуществляет система встроенного контроля, которая контролирует работоспособное состояние работающего на данном интервале времени объекта.

Сравнивая способы Структурного резервирования (рис. 4 и рис. 5), можно сделать следующие выводы:

1)в схеме рис. 4 быстро истощается ресурс работы как основной, так и резервной системы;

2) в схеме рис. 5 ресурс работы системы увеличивается, но необходимостью использования систем встроенного контроля и элементов коммутации надежность системы уменьшается за счет сложности данной системы.

2) по функциональному уровню резервирования различают следующие способы:

- общее резервирование, то есть резервируется система в целом;

- раздельное резервирование, то есть резервируются отдельные элементы с различными кратностями резервирования m;

3) по состоянию резервированных объектов различают:

- нагруженный (горячий) резерв. При этом резервные объекты работают в том же режиме, что и основные;

- ненагруженный (холодный) резерв. При этом резервные объекты отключены от нагрузки;

- облегченный (дежурный) резерв. При этом резервные объекты подключены к маломощному эквиваленту нагрузки.

Дата добавления: 2014-01-20