Закон проекции телесного угла

Законы архитектурной светофизики

Освещенность в какой-либо точке помещения создается световым потоком, который излучается с участков небосвода, видимых из данной точки через светопроемы, расположенные в ограждающих конструкциях здания. При этом возникает вопрос, от каких параметров зависят светотехнические показатели и каким образом их можно определить. Это позволяет сделать четыре основных закона строительной светотехники, которые формируют теоретическую базу данной науки.

Поместим помещение с расчетной точкой М под небосвод, который представляет собой полусферу единичного радиуса (рис. 7). Причем точка М совпадает с центром полусферы.

Для упрощения вывода закона примем следующие три допущения:

1) яркость неба во всех точках одинакова;

2) влияние отраженного света от внутренних поверхностей помещения не учитывается; 3) оконное заполнение светопроема отсутствует.

Освещенность в точке М создается видимым из т. М через проем сферическим прямоугольником АБВГ (рис. 7) площадью S. В этом прямоугольнике вырежем бесконечно малый точечный элемент dS с силой света dI. На основании формулы (6) определяем яркость этого элемента

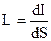откуда dI = L× dS.

Поскольку направление излучения от элемента dS до точки М перпендикулярно элементарной площадке, то b = 0 и cosb = 1.

Освещенность в т. М согласно формуле (5) для точечного источника света определится следующим образом:

.

Подставляя dI из предыдущего выражения, получаем

.

Однако, величина dS / R² = dw, согласно формулы (2), а величина dS × cos a / R² = ds есть проекция элементарного телесного угла на освещаемую плоскость. При интегрировании до конечных размеров светопроемов ds = s.

Таким образом,

Е_М = L× s. (9)

На основании этого выражения закон проекции телесного угла можно сформулировать следующим образом.

Дата добавления: 2014-01-20