Закон эффективности светопроемов

Закон светотехнического подобия

Освещенность в какой-либо точке поверхности помещения, создаваемая равномерно светящимся небосводом, прямо пропорциональна яркости неба L и площади проекции телесного угла s, в пределах которого из данной точки виден участок неба, на освещаемую поверхность.

На основании этого закона можно вычислить значение КЕО в точке М. Освещенность в этой точке под открытым небосводом с использованием формулы (9) будет равна:

Е_н = L× s_н = L × p × R²,

т.к. площадь проекции всей полусферы на горизонтальную плоскость s_н = p × R², а при единичном радиусе s_н = p. Тогда, Е_н = L × p. Подставляем значения двух освещенностей в формулу (7)

= 100 = 100, (10)

т.е. при равноярком небосводе величина КЕО прямопропорциональна площади проекции телесного угла светопроема.

Рис. 7. Схема к закону проекции телесного угла

Практическое значение этого закона очень велико: пользуясь им, можно сравнивать освещенности, создаваемые одним и теме же светопроемом, расположенным различно относительно рабочей плоскости, а также определять светотеневой рисунок на объемных объектах и деталях под открытым небосводом в пасмурный день.

На основе этого закона разработан ряд графических и аналитических методов расчета естественного освещения (в частности, метод Данилюка), получившие широкое распространение в нашей и мировой архитектурной практике.

Рассмотрим освещенность в точке М, создаваемую несколькими светящимися поверхностями, имеющими яркости L₁, L₂, …, L_к и площади проекции телесных углов на освещаемую плоскость w₁, w₂,…, w_к. Тогда освещенности от этих поверхностей в данной точке будут равны:

Е₁ = L₁· w₁; Е₂ = L₂·w₂; ….; Е_к = L_к·w_к.

Условие, когда эти поверхности создадут равные освещенности, т.е. Е₁ = Е₂ = … = Е_к, будет соблюдено, если L₁·w₁ = L₂·w₂ = … = L_к·w_к.

Если принять полусферу равномерной яркости, то w₁ = w₂ = … = w_к.

Рис. 8. Схема к закону све- тотехнического по- добия

Отсюда видно, что светящиеся поверхности – светопроемы – могут иметь различные размеры при одинаковом значении площади проекции телесного угла, описанного из т. М по контурам этих проемов.

Из всего этого следует, что освещенность в точке от светящейся поверхности зависит не от абсолютных ее размеров, а от относительных.

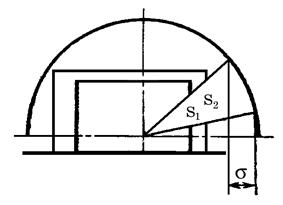
Или, светящиеся равнояркие поверхности разных размеров могут создать в точке одинаковую освещенность, если площади проекции их телесных углов, описанных из точки по их контуру, будут равны. На схеме (рис. 8) представлены два светопроема. Хотя абсолютные их размеры различны S₂ > S₁, но s₁ = s₂ = s, поэтому и освещенности от этих двух светопроемов будут равны. Это и есть формулировки закона светотехнического подобия.

Светопроемы, плоскость остекления которых располагаются параллельно освещаемой плоскости, имеют наибольшую световую активность по отношению к светопроемам, имеющим какой-либо угол наклона.

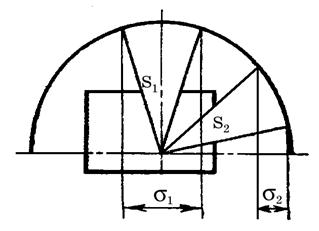На схеме (рис. 9) представлено помещение с двумя одинаковыми по размерам светопроемами, один из которых расположен в стене, другой в покрытии. Причем, расстояние от расчетной точки до центров проемов равны. Из схемы видно, при равенстве размеров проемов S₁ = S₂, проекции телесных углов на освещаемую плоскость различны s₁ > s₂, поэтому освещенность от светопроема, расположенного в покрытии, будет гораздо больше освещенности от светопроема, расположенного в стене. Отсюда следует, что зенитные фонари обладают наибольшей световой активностью, т.к. плоскость их остекления параллельна освещаемой плоскости.

Практическое значение этого закона заключается в том, что сразу можно определить относительную световую эффективность светопроемов одинаковой площади, расположенных под различными углами наклона.

Дата добавления: 2014-01-20