Линейчатые поверхности

Линейчатые поверхности образуются непрерывным движением прямой образующей по некоторой направляющей, которая может быть прямой, ломаной или кривой линией.

1. Линейчатые поверхности с одной направляющей

и т-кой (вершиной)

Эти поверхности образуются движением прямой образующей, один конец которой проходит через неподвижную т-ку S, а второй - перемещается по направляющей m. В зависимости от того, какой линией является направляющая, образуется тот или иной вид поверхности.

Определитель такой поверхности имеет вид: Σ (S, m),

где S – конечная т-ка, m – направляющая.ъ

Поверхности, образующиеся в данной группе:

а) коническая поверхность образуется движением прямолинейной образующей ℓ, по криволинейной направляющей m и проходящей через одну фиксированную т-ку (вершину) S.

б) пирамидальная поверхность образуется движением прямолинейной образующей ℓ по ломаной направляющей m и проходящей через одну фиксированную т-ку (вершину) S.

в) цилиндрическая поверхность образуется движением прямолинейной образующей ℓ, по криволинейной направляющей m, при условии, что S бесконечно удалена. (т.е. все образующие двигаются относительно друг-друга параллельно)

г) призматическая поверхность образуется движением прямолинейной образующей ℓ по ломаной направляющей m, при этом S бесконечно удалена.

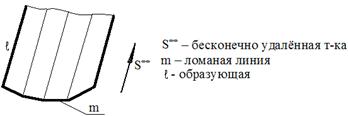
2. Поверхности, образованные 2-мя направляющими и пл-тью параллелизма

Поверхности данной группы образуются при движении в пространстве прямой образующей ℓ по двум направляющим m и n, оставаясь при этом параллельной заданной пл-ти Г, которая называется пл-тью параллелизма.

В данную группу входят следующие поверхности:

а) цилиндроид – поверхность, образованная движением прямой образующей ℓ ||-но плоскости параллелизма Г по двум криволинейным направляющим m и n, не лежащим в одной плоскости.

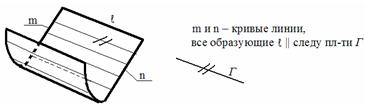
б) коноид образуется движением прямой образующей ℓ ||-но плоскости параллелизма Г по двум направляющим m и n, одна из которых является прямой линией, а вторая – какой-либо кривой.

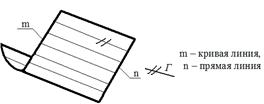
в) гиперболический параболоид (гипар) образуется движением прямолинейной образующей ℓ ||-но плоскости параллелизма Г по двум прямолинейным направляющим m и n, представляющие собой две скрещивающиеся прямые.

Рассмотрим решение задач.

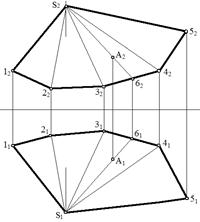
Задача 1: По заданному определителю построить каркас и очерк поверхности. Построить недостающую пр-ию т-ки А, принадлежащую данной поверхности.

Решение:

Итак, поверхность задана определителем Σ (S, m), S-конечная точка, проекция направляющей – ломаная линия, следовательно, это пирамидальная поверхность.

Дата добавления: 2014-01-20