Движение материальной точки по окружности

В случае движение материальной точки по окружности, по аналогии с линейной скоростью и ускорением, вводятся угловая скорость и ускорение.

Пусть точка движется по окружности радиуса (рис. 1.4.1). Ее положение через малый промежуток времени 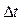зададим углом 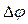. Элементарные, то есть бесконечно малые повороты можно рассматривать как векторы (их обозначают или ), модуль которых равен углу поворота, а направление совпадает с направлением поступательного движения острия буравчика (винта), рукоятка которого вращается в направлении движения точки по окружности. Вектор поворота является так называемым аксиальным вектором и не имеет определенной точки приложения (его можно откладывать из любой точки оси вращения).

Угловой скоростью называется векторная величина, равная первой производной угла поворота по времени:

. (1.4.1)

Направление вектора угловой скорости , так же, как и вектора угла поворота , задается правилом буравчика: вектор угловой скорости совпадает по направлению с поступательным движением острия буравчика, рукоятка которого вращается в направлении движения точки по окружности.

Размерность угловой скорости .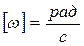

Зная угловую скорость 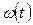, можно найти угол поворота точки .

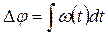Линейная скорость точки (скорость движения вдоль траектории)

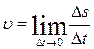
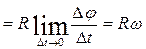. (1.4.2)

1) Если 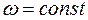, то движение будет равномерным и его можно характеризовать периодом вращения – временем, за которое точка совершает один полный оборот:

. (1.4.3)

Число полных оборотов, совершаемых точкой в единицу времени, называется

частотой вращения:

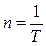. (1.4.4)

Учитывая 1.4.3,

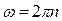. (1.4.5)

Размерность частоты .

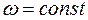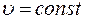Поскольку , то и .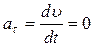

Поэтому полное ускорение точки

. (1.4.6)

Пример 1.4.1 Линейная скорость 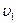точек на окружности вращающегося диска равна . Точки, расположенные на ближе к оси, имеют линейную скорость 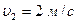. Определить частоту вращения диска.

Дано: Решение:

Искомая частота (по 1.4.4) . Т.к. (по 1.4.3) , где 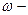угловая скорость, то . Линейная скорость точек, лежащих на разных расстояниях от оси вращения диска, различна, но угловая скорость одинакова. Учитывая это и формулу 1.4.2, можно составить систему уравнений

Решим совместно систему уравнений:

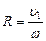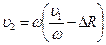; ; , откуда .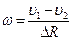

Подставим в формулу для искомой частоты: .

Ответ: .

2) Если 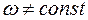, то движение будет неравномерным и можно ввести понятие углового ускорения.

Угловое ускорение – это векторная величина, равная первой производной угловой скорости по времени:

. (1.4.8)

Вектор углового ускорения направлен по оси вращения (при ускоренном движении параллелен , при замедленном – антипараллелен ).

Тангенциальная составляющая ускорения:

. (1.4.9)

Нормальная составляющая ускорения:

. (1.4.10)

Зная угловое ускорение 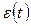, можно найти угловую скорость точки

.

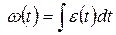В случае равнопеременного движения точки по окружности ():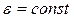

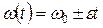и , (1.4.11)

где начальная угловая скорость, 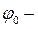угол поворота тела при .

Представим в виде таблицы соотношения, описывающие поступательное и вращательное движения, сопоставив их кинематические характеристики.

Таблица 1.4.1.

Дата добавления: 2014-01-20