Из одной системы отсчета в другую

Преобразования скорости и ускорения при переходе

В рамках классической механики скорость и ускорение тела преобразуются по определенным правилам при переходе от одной системы отсчета к другой.

Пусть имеются две произвольные системы отсчета 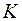и 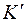(рис. 1.5.1). Известны скорость 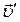и ускорение 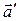тела (точки А) в 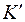-системе. Рассмотрим случай, когда 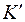-система движется поступательно по отношению к 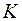-системе, и определим значения скорости 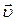и ускорения 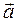тела в 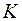-системе.

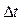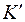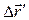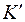Если за время тело (точка А) переместилась относительно -системы на величину , а -система переместилась относительно 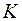-системы на 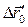, то по правилу векторного сложения следует, что перемещение 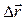тела относительно 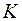-системы будет равно 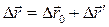. Разделив обе части этого равенства на 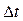и обозначив через 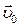скорость 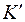-системы относительно 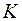-системы, получим: .

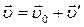Рассуждая аналогично, найдем формулу преобразования ускорения: 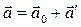, из которой вытекает важное следствие: при 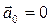ускорения 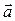и 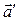равны. Иными словами, если система отсчета 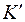движется поступательно, без ускорения относительно системы отсчета 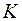, то ускорения тела в обеих системах отсчета будут одинаковы. Этот факт имеет важное значение при изучении механического движения. Переход из одной системы отсчета в другую довольно часто применяется на практике и порой существенно облегчает решение физических задач.

Часто встречаются задачи, в которых два тела движутся независимо друг от друга в некоторой системе отсчета, и требуется определить какие-либо величины (перемещение, скорость), характеризующие движение одного тела относительно другого. В таких случаях, как правило, удобно перейти в систему отсчета, связанную с тем телом, относительно которого рассматривается движение другого тела, и применить полученные выше формулы преобразований. После несложных рассуждений можно установить, что относительное перемещение и относительная скорость двух тел определяются векторной разностью их перемещений и скоростей, заданных по отношению к одной и той же(чаще всего – неподвижной) системе отсчета.

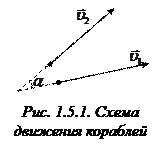
Пример 1.5.1. Два корабля движутся с постоянными скоростями и 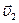под углом 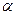друг к другу (рис.1.5.1). Найти скорость первого корабля относительно второго.

Дано: Решение:

Перейдем в систему отсчета, связанную со вторым кораблем, движущимся со скоростью 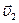. В этой системе отсчета скорость 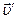первого корабля будет равна .

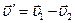Вектор 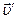определим геометрически, используя правило построения векторной разности (рис. 1.5.2).

Из треугольника 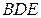с помощью теоремы косинусов найдем модуль искомого вектора: .

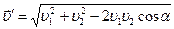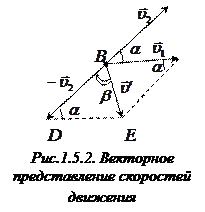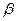Направление вектора зададим углом , который определим из 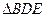по теореме синусов: .

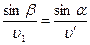Отсюда .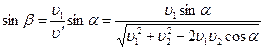

Ответ: , .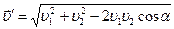

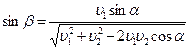Глава 2. Динамика поступательного движения

Динамика рассматривает причины изменения скорости движения тел и устанавливает законы движения. В основе динамики лежат три закона Ньютона.

Дата добавления: 2014-01-20