Закон сохранения механической энергии

С одной стороны, работа консервативных сил равна изменению кинетической энергии тела 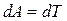. С другой стороны, эта же работа равна убыли потенциальной энергии 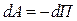. Поэтому 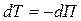, следовательно, 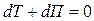и

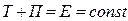. (3.3.1)

Это выражение представляет собой закон сохранения полной механической энергии: в замкнутой системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется, т.е. не изменяется со временем.

В таких системах могут происходить лишь превращения кинетической энергии в потенциальную и обратно в эквивалентных количествах. Поэтому этот закон не есть просто закон количественного сохранения энергии, а закон сохранения и превращения энергии, выражающий качественную сторону взаимного превращения различных форм движения друг в друга. Закон сохранения и превращения энергии – фундаментальный закон природы (он справедлив как для систем макроскопических тел, так и для систем микротел, подчиняющихся законам квантовой механики).

В замкнутой системе, в которой действуют также диссипативные силы, и в незамкнутой системе, полная механическая энергия не сохраняется. Изменение полной механической энергии системы при переходе из состояния 1 в состояние 2 равно работе 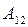, совершенной при этом внешними или внутренними диссипативными силами: 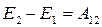. Последнее выражение отражает закон изменения энергии. Следовательно, в этих случаях закон сохранения механической энергии несправедлив. Однако при «исчезновении» механической энергии всегда возникает эквивалентное количество энергии другого вида (например, тепловой). Таким образом, энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой. В этом заключается физическая сущность закона сохранения и превращения энергии – сущность неуничтожимости материи и ее движения.

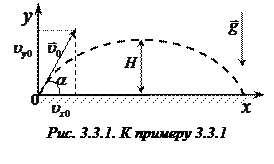
Пример 3.3.1. Камень брошен вверх под углом 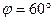к горизонту. Кинетическая энергия камня в начальный момент времени равна 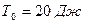. Определить кинетическую и потенциальную энергию камня в высшей точке его траектории. Сопротивлением воздуха пренебречь.

Дано: Решение:

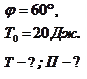
Сделаем чертеж. Укажем направление вектора начальной скорости 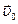и направление ускорения 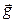(рис. 3.3.1).

Кинетическая энергия камня в произвольный момент времени равна 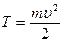, где скорость камня 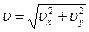. В наивысшей точке траектории 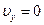, следовательно, 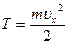. Вдоль оси Ох движение камня равномерное, и в любой момент времени 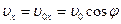. Т.е., 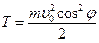. С учетом того, что в начальный момент времени кинетическая энергия 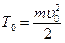, искомая кинетическая энергия камня в высшей точке траектории .

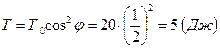Потенциальная энергия камня в наивысшей точке траектории 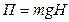, где 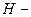максимальная высота подъема камня. Запишем кинематические уравнения движения камня вдоль оси Оу: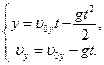В наивысшей точке 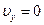, 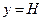. Таким образом, 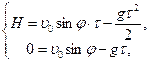где 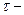время подъема камня до наивысшей точки. Решая совместно систему уравнений, находим, что 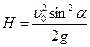. Поэтому искомая потенциальная энергия камня в наивысшей точке траектории .

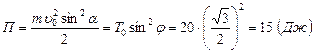Примечание. Потенциальную энергию камня в наивысшей точке траектории можно найти по закону сохранения полной механической энергии системы.

Рассмотрим два состояния системы: момент бросания камня (на поверхности земли) – состояние 1 и в наивысшей точке траектории – состояние 2. Система замкнута, и в ней действуют только консервативные силы. Поэтому полная механическая энергия в двух состояниях одинакова: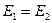. Поскольку полная энергия складывается из кинетической и потенциальной, то .

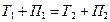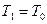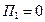Учитывая, что в момент бросания , а , то .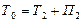

Кинетическая энергия камня в наивысшей точке траектории 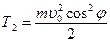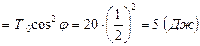. Следовательно, потенциальная энергия камня в этой точке .

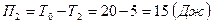Ответ: ,.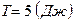

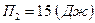Пример 3.3.2. На рельсах стоит платформа, на которой в горизонтальном положении закреплено орудие без противооткатного устройства. Из орудия произведен выстрел вдоль железнодорожного пути. Масса снаряда 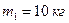, его скорость 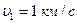. Масса платформы с орудием 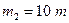. На какое расстояние 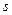откатится платформа после выстрела, если коэффициент сопротивления ?

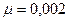Дано: Решение: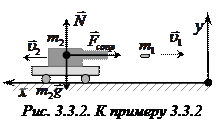

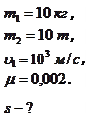
Сделаем чертеж. Укажем направление скоростей снаряда и платформы с орудием 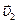после выстрела, а также сил, действующих на платформу в процессе движения (рис. 3.4.9). В момент выстрела систему «платформа с орудием – снаряд» можно считать замкнутой (диссипативные силы не действуют), поэтому выполняется закон сохранения импульса. Учитывая, что до выстрела платформа и снаряд покоились (импульс системы был равен нулю), закон сохранения импульса (в векторной форме) имеет вид: .

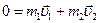Спроецируем это векторное уравнение на ось Ох: 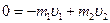, откуда выразим скорость платформы с орудием сразу после выстрела .

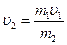На платформу с орудием в процессе ее движения действует внешняя сила сопротивления 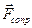. Следовательно, система «платформа с орудием» является незамкнутой и в ней выполняется закон превращения механической энергии: изменение полной механической энергии системы равно работе внешних сил. Т.к. потенциальная энергия платформы равна 0, то 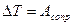, где 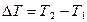(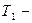начальная кинетическая энергия платформы, 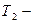конечная кинетическая энергия платформы); 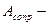работа сил сопротивления.

Учитывая, что 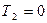(платформа, пройдя путь 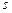, остановилась), а 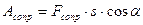, где 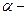угол между направлением действия силы и направлением скорости движения платформы 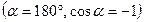, можно записать 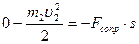, откуда .

Найдем силу сопротивления 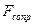. Запишем второй закон Ньютона в векторной форм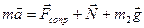е: , где 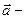ускорение платформы, 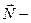сила нормальной реакции опоры, 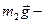сила тяжести. Спроецируем это векторное уравнение на ось Оу: 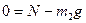, откуда 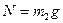. Учитывая, что 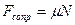, получим .

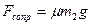Подставим найденные значения 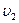и 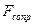в выражение для искомого расстояния : .

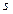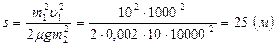Ответ: .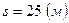

Дата добавления: 2014-01-20