
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Абсолютно упругий и неупругий центральный удар
|
|
|
|
Проиллюстрируем применение законов сохранения импульса и энергии на примере удара тел.
Удар (или соударение) – это столкновение двух или более тел, при котором взаимодействие длится очень короткое время.
При ударе в телах возникают значительные внутренние силы, поэтому внешними силами, действующими на них, можно пренебречь и рассматривать соударяющиеся тела как замкнутую систему, применяя к ней законы сохранения.
Во время удара тела деформируются и кинетическая энергия относительного движения соударяющихся тел преобразуется в энергию упругой деформации. Во время удара происходит перераспределение энергии между соударяющимися телами, но относительная скорость тел после удара не достигает своего прежнего значения (нет идеально упругих тел и идеально гладких поверхностей). Отношение нормальных составляющих относительной скорости тел после и до удара называется коэффициентом восстановления  :
:
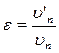 . (3.4.1)
. (3.4.1)
Если 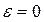 , то тела называют абсолютно неупругими, если
, то тела называют абсолютно неупругими, если  – абсолютно упругими. Для большинства реальных тел
– абсолютно упругими. Для большинства реальных тел 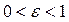 . Например, для шаров из слоновой кости
. Например, для шаров из слоновой кости  , для медных шаров
, для медных шаров 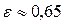 , для свинцовых
, для свинцовых  .
.
Прямая, проходящая через точку соприкосновения тел перпендикулярно к поверхности их соприкосновения, называется линией удара.

 |
Удар называют центральным, если тела до удара движутся вдоль прямой, проходящей через их центры масс.
Абсолютно упругий центральный удар – столкновение двух тел, в результате которого во взаимодействующих телах не остается деформаций, а вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию.
В этом случае выполняются закон сохранения импульса и закон сохранения кинетической энергии. Пусть шары массами  и
и  имели до удара скорости
имели до удара скорости 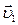 и
и  соответственно. После удара их скорости стали
соответственно. После удара их скорости стали 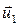 и
и 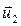 . Направления скоростей до удара показаны на рис. 3.4.1, после удара – на рис. 3.4.2. Запишем закон сохранения импульса (в проекции на ось Ох) и закон сохранения кинетической энергии:
. Направления скоростей до удара показаны на рис. 3.4.1, после удара – на рис. 3.4.2. Запишем закон сохранения импульса (в проекции на ось Ох) и закон сохранения кинетической энергии:
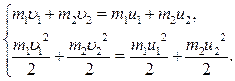
Произведем преобразование 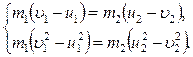
Откуда: 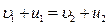 ,
,  и
и  .
.
Проанализируем эти формулы.
1. Пусть 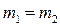 . Тогда
. Тогда 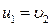 и
и  . Следовательно, при ударе шаров с равной массой они «обмениваются» скоростями.
. Следовательно, при ударе шаров с равной массой они «обмениваются» скоростями.
2. Пусть  (второй шар покоится). Тогда
(второй шар покоится). Тогда 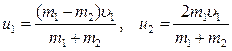 .
.
а) Если  , то
, то 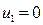 и
и 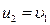 . Следовательно, первый шар после удара остановится, а второй будет двигаться с той же скоростью и в том же направлении, в котором двигался до удара первый шар.
. Следовательно, первый шар после удара остановится, а второй будет двигаться с той же скоростью и в том же направлении, в котором двигался до удара первый шар.
б) Если  , то
, то 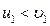 и
и  . Следовательно, первый шар будет двигаться после удара в прежнем направлении, но с меньшей скоростью. Скорость второго шара после удара будет больше, чем первого шара, и он будет двигаться в том же направлении, в котором двигался до удара первый шар.
. Следовательно, первый шар будет двигаться после удара в прежнем направлении, но с меньшей скоростью. Скорость второго шара после удара будет больше, чем первого шара, и он будет двигаться в том же направлении, в котором двигался до удара первый шар.
в) Если  , то
, то 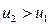 по модулю и проекция
по модулю и проекция 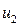 на направление оси
на направление оси 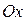 отрицательна. Следовательно, направление движения первого шара изменится – он отскакивает обратно. Скорость второго шара после удара будет меньше, чем первого, и он будет двигаться в том же направлении, в котором двигался до удара первый шар.
отрицательна. Следовательно, направление движения первого шара изменится – он отскакивает обратно. Скорость второго шара после удара будет меньше, чем первого, и он будет двигаться в том же направлении, в котором двигался до удара первый шар.
г) Если  (столкновение шара со стеной), то
(столкновение шара со стеной), то 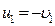 и
и 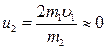 .
.
Следовательно, первый шар упруго отскакивает от стены и меняет направление своего движения на противоположное.
Абсолютно неупругий центральный удар – столкновение двух тел, в результате которого тела начинают двигаться как единое целое.
Пусть шары массами  и
и  имели до неупругого удара скорости
имели до неупругого удара скорости  и
и 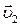 соответственно. После удара они стали двигаться как одно целое со скоростью
соответственно. После удара они стали двигаться как одно целое со скоростью  . Направления скоростей до удара показаны на рис. 3.4.3, после удара – на рис. 3.4.4. При
. Направления скоростей до удара показаны на рис. 3.4.3, после удара – на рис. 3.4.4. При
абсолютно неупругом ударе выполняется только закон сохранения импульса:
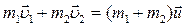 .
.
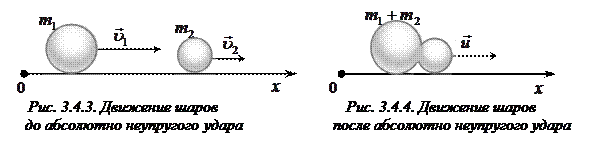
Спроецируем это векторное уравнение на ось 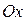 :
: 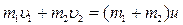 , откуда
, откуда
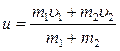 .
.
Если шары двигались навстречу друг другу, то они вместе будут продолжать двигаться в ту сторону, в которую двигался шар с большим импульсом.
В частном случае, если  , то
, то  .
.
Закон сохранения кинетической энергии не выполняется, т.к. в процессе взаимодействия шаров между ними действуют силы, зависящие от скорости движения (этим они похожи на силы сопротивления), являющиеся диссипативными. Часть кинетической энергии переходит во внутреннюю. «Потеря» кинетической энергии
вследствие деформации равна:  . Подставляя найденное значение
. Подставляя найденное значение 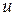 , получим
, получим  .
.
Проанализируем полученные формулы.
1. Если второе тело покоилось 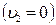 , то скорость шаров после удара
, то скорость шаров после удара 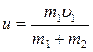 . Во внутреннюю энергию переходит энергия
. Во внутреннюю энергию переходит энергия 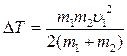 .
.
2. Если 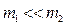 (молот и наковальня), то
(молот и наковальня), то 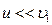 , поэтому вся кинетическая энергия молота переходит в энергию деформаций куска металла (поковки), лежащей между молотом и наковальней.
, поэтому вся кинетическая энергия молота переходит в энергию деформаций куска металла (поковки), лежащей между молотом и наковальней.
3. Если  (молоток и гвоздь), то
(молоток и гвоздь), то 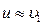 и практически вся кинетическая энергия молотка затрачивается на перемещение гвоздя, а не на его деформацию.
и практически вся кинетическая энергия молотка затрачивается на перемещение гвоздя, а не на его деформацию.

 Пример 3.4.1. Шар массой
Пример 3.4.1. Шар массой  , движущийся горизонтально с некоторой скоростью
, движущийся горизонтально с некоторой скоростью  , столкнулся с неподвижным шаром массы
, столкнулся с неподвижным шаром массы  . Шары абсолютно упругие, удар прямой. Какую долю
. Шары абсолютно упругие, удар прямой. Какую долю 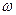 своей кинетической энергии первый шар передал второму?
своей кинетической энергии первый шар передал второму?
 Дано: Решение:
Дано: Решение:

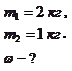 Сделаем чертеж. Укажем направление скорости первого шара до удара (рис. 3.4.5) и возможные направления скоростей шаров после удара (рис. 3.4.6) (если направление выбрано неверно, то скорость получится со знаком «–»).
Сделаем чертеж. Укажем направление скорости первого шара до удара (рис. 3.4.5) и возможные направления скоростей шаров после удара (рис. 3.4.6) (если направление выбрано неверно, то скорость получится со знаком «–»).
 Доля энергии, переданной первым шаром второму:
Доля энергии, переданной первым шаром второму:  , где
, где 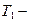 кинетическая энергия первого шара до удара;
кинетическая энергия первого шара до удара;  ,
, 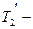 скорость и кинетическая энергия второго шара после удара.
скорость и кинетическая энергия второго шара после удара.
Для нахождения  воспользуемся тем, что при абсолютно упругом ударе одновременно выполняются законы сохранения импульса (закон сохранения импульса записан в проекции на ось Ох) и
воспользуемся тем, что при абсолютно упругом ударе одновременно выполняются законы сохранения импульса (закон сохранения импульса записан в проекции на ось Ох) и
кинетической энергии: 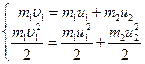 .
.
Решая совместно эти уравнения, найдем  , следовательно,
, следовательно, 
 .
.
Таким образом, доля переданной энергии зависит только от масс сталкивающихся шаров и не изменится, если шары поменяются местами.
Ответ:  .
.
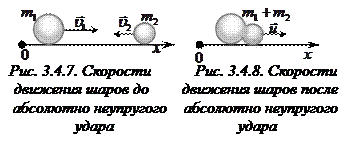 Пример 3.4.2. Два шара массами
Пример 3.4.2. Два шара массами 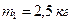 и
и  движутся навстречу друг другу со скоростями
движутся навстречу друг другу со скоростями  и
и  . Удар неупругий. Определить: 1) скорость шаров
. Удар неупругий. Определить: 1) скорость шаров 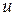 после удара; 2) долю
после удара; 2) долю 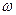 кинетической энергии шаров, превратившуюся во внутреннюю энергию.
кинетической энергии шаров, превратившуюся во внутреннюю энергию.
 Дано: Решение:
Дано: Решение:

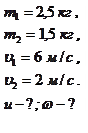 Сделаем чертеж. Укажем направление скоростей шаров до удара (рис. 3.4.7) и после удара (рис. 3.4.8). Выполняется только закон сохранения импульса
Сделаем чертеж. Укажем направление скоростей шаров до удара (рис. 3.4.7) и после удара (рис. 3.4.8). Выполняется только закон сохранения импульса 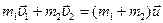 . Спроецируем векторное уравнение на ось Ох:
. Спроецируем векторное уравнение на ось Ох: 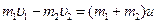 . Следовательно, скорость шаров после неупругого удара равна
. Следовательно, скорость шаров после неупругого удара равна 
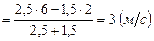 . Кинетическая энергия шаров до удара
. Кинетическая энергия шаров до удара 
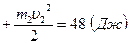 , после удара
, после удара  .
.
В результате неупругого удара шаров их кинетическая энергия уменьшается, за счет чего увеличивается их внутренняя энергия.
Долю кинетической энергии, пошедшей на увеличение их внутренней энергии, определим из соотношения  .
.
Ответ:  ,
, 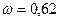 .
.
Пример 3.4.3. Молот массой 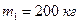 падает на поковку, масса которой вместе с наковальней
падает на поковку, масса которой вместе с наковальней 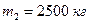 . Скорость молота в момент удара равна
. Скорость молота в момент удара равна 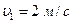 . Найти: а) кинетическую энергию молота в момент удара
. Найти: а) кинетическую энергию молота в момент удара  ; б) энергию, переданную фундаменту
; б) энергию, переданную фундаменту 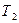 ; в) энергию, затраченную на деформацию поковки
; в) энергию, затраченную на деформацию поковки 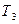 ; г) к.п.д.
; г) к.п.д. 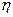 удара молота о поковку. Удар молота рассматривать как неупругий.
удара молота о поковку. Удар молота рассматривать как неупругий.
 Дано: Решение:
Дано: Решение:

 а) Кинетическую энергию молота в момент удара найдем по формуле
а) Кинетическую энергию молота в момент удара найдем по формуле 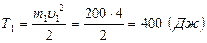 .
.
б) Чтобы найти энергию, переданную фундаменту, найдем скорость системы молот – поковка (с наковальней) непосредственно после удара. Запишем закон сохранения импульса, который выполняется при неупругом ударе, в проекции на ось  (положительное направление оси совпадает с направлением движения молота)
(положительное направление оси совпадает с направлением движения молота) 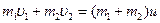 , где
, где 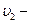 скорость поковки (с наковальней) перед ударом,
скорость поковки (с наковальней) перед ударом,  скорость молота и поковки (вместе с наковальней) после удара. Учитывая, что до удара поковка покоилась
скорость молота и поковки (вместе с наковальней) после удара. Учитывая, что до удара поковка покоилась  , находим, что
, находим, что 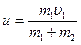 . В результате сопротивления фундамента скорость
. В результате сопротивления фундамента скорость 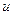 быстро гасится, а кинетическая энергия, которой обладает система молот – поковка (с наковальней), передается фундаменту. Следовательно, энергия, переданная фундаменту
быстро гасится, а кинетическая энергия, которой обладает система молот – поковка (с наковальней), передается фундаменту. Следовательно, энергия, переданная фундаменту 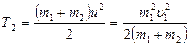 . Поскольку
. Поскольку  , запишем
, запишем 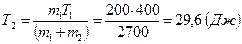 .
.
в) Молот до удара обладал энергией 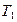 . Энергия, переданная фундаменту
. Энергия, переданная фундаменту  . Следовательно, на деформацию поковки использовалась энергия
. Следовательно, на деформацию поковки использовалась энергия 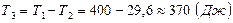 .
.
г) Назначение молота – вызвать деформацию поковки. Следовательно, энергию  следует считать полезной. Таким образом,
следует считать полезной. Таким образом,  , т.е.
, т.е.  .
.
Ответ:  ,
, 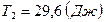 ,
,  ,
,  .
.
 Пример 3.4.4. Молотком, масса которого
Пример 3.4.4. Молотком, масса которого 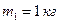 , забивают в стену гвоздь массой
, забивают в стену гвоздь массой  . Определить к.п.д.
. Определить к.п.д. 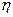 удара молотка.
удара молотка.
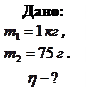 Решение:
Решение:
 Определим энергию, затраченную на углубление гвоздя в стену. Предварительно найдем скорость системы молоток – гвоздь непосредственно после удара. Запишем закон сохранения импульса в проекции на ось Ох (положительное направление оси совпадает с направлением движения молотка):
Определим энергию, затраченную на углубление гвоздя в стену. Предварительно найдем скорость системы молоток – гвоздь непосредственно после удара. Запишем закон сохранения импульса в проекции на ось Ох (положительное направление оси совпадает с направлением движения молотка): 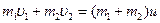 , где
, где  скорость молотка до удара,
скорость молотка до удара, 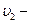 скорость гвоздя до удара,
скорость гвоздя до удара,  скорость молотка и гвоздя после удара.
скорость молотка и гвоздя после удара.
Гвоздь перед ударом покоился 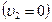 . Поэтому
. Поэтому 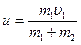 .
.
В результате сопротивления стены скорость молотка и гвоздя после удара быстро гасится, а кинетическая энергия, которой обладает система молоток – гвоздь, затрачивается на углубление гвоздя в стену.
Эту энергию находим по формуле  .
.
Т.к. молоток служит для забивания гвоздя в стену, то энергию  следует считать полезной. Учитывая, что энергия молотка в момент удара
следует считать полезной. Учитывая, что энергия молотка в момент удара  , то
, то  .
.
Искомый к.п.д.  , т.е.
, т.е.  .
.
Ответ:  .
.
 |
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 14657; Нарушение авторских прав?; Мы поможем в написании вашей работы!