Смешанные стратегии. Седловая точка в матричных играх всё-таки скорее исключение, чем правило

Седловая точка в матричных играх всё-таки скорее исключение, чем правило. А что же может гарантировать себе игрок, если седловой точки нет?

Давайте снова рассмотрим игру с платёжной матрицей

.

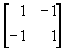Здесь , 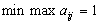и между 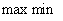и 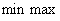образуется “дыра” 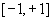Как можно её заполнить и чем?

Представим себя в позиции первого игрока. Он имеет гарантированный выигрыш (скорее, проигрыш), равный (-1). Как он может его повысить?

Конечно, если игра повторяется много раз, то он может изучить своего партнёра, придумывать всякие схемы игры и т.д. и т.п., но вряд ли это даст какие-то гарантии, если число партий невелико. Тут никакие схемы не помогут.

В такой ситуации единственный выход - выбирать свой ход случайным образом. Например, взять и подбросить монету. Упадёт она кверху орлом - делать ход i=1, выпадет решка - делать ход i=2. Что же это даст?

Выигрыш станет случайной величиной и оценивать его надо по математическому ожиданию. Пусть второй игрок делает ход j=1. Тогда математическое ожидание выигрыша первого игрока будет

.

Если второй игрок делает ход j=2, то математическое ожидание выигрыша первого игрока равно

.

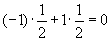Таким образом, выбирая свой ход случайно, первый игрок гарантирует себе (правда, в среднем, а не в каждой партии), выигрыш, равный нулю. А это всё-таки лучше, чем гарантированный выигрыш, равный (-1).

Аналогично, второй игрок, бросая монету и выбирая ход в соответствии с её “указанием”, гарантирует себе в среднем проигрыш, равный 0. Это тоже лучше, чем проигрыш, равный 1.

Таким образом, оказывается, что случайный выбор хода повышает наши шансы на успех, хотя бы в среднем. И это является одной из основных идей теории игр - выбиратьсвой ход случайно. Подобный случайный выбор хода получил название смешанной стратегии.

Конечно, с обычных житейских позиций, случайный выбор хода не всегда приемлем. Вообразите себе военачальника, который выиграл сражение. Он даёт интервью по TV и на вопрос о том, как же он принял правильное решение, говорит: “Ну, я бросил монету, она упала орлом кверху, и поэтому я … ”. Как посмотрит на него телезритель? А если он проиграл битву, то как отнесётся к такому ответу его начальство?

И тем не менее, случайный выбор хода - смешанная стратегия - имеет право на существование, даже в реальной жизни. Когда не знаешь, как действовать - выбирай свой ход случайным образом! Иногда помогает. По крайней мере, никто не разгадает стратегии твоего поведения и не предугадает твоего хода.

Дата добавления: 2014-01-20