Игры двух лиц с ненулевой суммой

Рассмотрим теперь основные идеи, касающиеся игр двух лиц с ненулевой суммой. В этом случае игра задаётся двумя матрицами, которые обычно объединяют в одну и пишут в виде

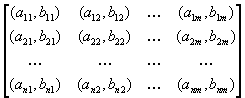
Здесь 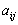- выигрыш первого игрока и - выигрыш второго, если первый игрок делает ход i, а второй - j. Однако в данном случае

В такой ситуации появляется принципиально новый момент, которого не было раньше - возможность сговора, совместных действий игроков. Когда 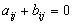, то интересы обоих игроков прямо противоположны и возможность сговора исключена в силу противоположности интересов. Если , то интересы игроков могут хотя бы частично совпадать, что и определяет возможность хотя бы частичного сотрудничества между ними.

И эта возможность сговора не упрощает, а сильно усложняет ситуацию! Потому, что до чего и как договорятся игроки в очень сильной степени зависит от двух вещей: от самой возможности вести переговоры и от психологических особенностей игроков. А психология - очень сложная вещь и математика до неё еще не добралась.

Игры двух лиц с ненулевой суммой принято разбивать на два класса - некооперативные и кооперативные. В некооперативных играх игроки не имеют возможности общаться друг с другом. Как же они могут договориться между собой? Это возможно, если игра повторяется - тогда возможность такого сговора появляется в ходе повторения игры, ведь можно наказывать партнёра, выбирая заведомо плохой для него ход. Но вот что из этого получится - теория игр пока не даёт ни ответа, ни совета.

В кооперативных играх игроки имеют возможность договариваться в любое удобное для них время и никаких косвенных приёмов для договорённостей им применять не надо.

Дата добавления: 2014-01-20