Симметрические полиномы

Формулы Виета

Теорема 2.17 (Формулы Виета) Пусть многочлен 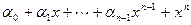имеет корни 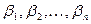. Тогда .

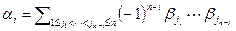Определение 2.4Многочленом от n переменных называется функция вида 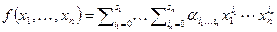. Степенью многочлена называется максимальная суммарная степень по всем переменным. Слагаемое вида 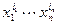называется мономом.

Многочлен от n переменных может содержать несколько мономов максимальной степени. Моном максимальной степени 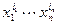назовём старшим, если набор его степеней 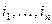лексикографически максимален. Обозначим через v(f) набор степеней максимального монома. Имеет место

Лемма 2.2 v(fg)=v(f)+v(g),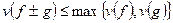

Доказательство вытекает из определения.

Определение 2.5Многочлен от нескольких переменных называется симметрическим, если он не меняется при любой перестановке переменных.

Определение 2.6Многочлены 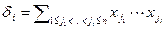, где i=1,…,n называются элементарными симметрическими многочленами.

Коэффициенты многочлена с точностью до знака суть значения элементарных симметрических многочленов от его корней.

Заметим .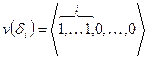

Лемма 2.3 Пусть f - симметрический многочлен и 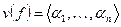, тогда .

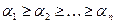Доказательство. Если найдётся i, при котором 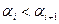, то переставим 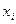и 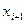. В результате получим более старший моном.

Лемма 2.4 Пусть 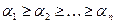- набор целых неотрицательных чисел. Тогда .

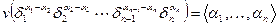Доказательство проводится непосредственно проверкой.

Теорема 2.18 (Основная теорема алгебры симметрических многочленов)

Любой симметрический многочлен единственным образом представляется в виде полинома от элементарных симметрических многочленов.

Доказательство. Пусть 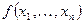- симметрический многочлен и 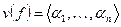. Обозначим через коэффициент при старшем мономе f и положим 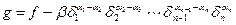. Многочлен g симметрический и v(g) лексикографически меньше v(f). Следовательно, через конечное число шагов он станет равный нулю и f выразится в виде полинома от элементарных симметрических многочленов.

Допустим, существуют два разных представления 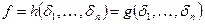. Разность f-g - не нулевой многочлен от элементарных симметрических многочленов, но при выражении элементарных симметрических многочленов через переменные он должен обратиться в 0.

Выделим член 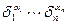, у которого величина 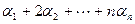максимальная. Если таких членов несколько, то из них выберем такое, на котором набор 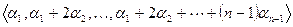лексикографически максимален. Набор, отвечающий данным условиям единственен. При подстановке переменных вместо элементарных симметрических полиномов именно этот набор даст старший моном. Причём это моном входит только в единственное слагаемое. Следовательно, найдётся моном с отличным от нуля коэффициентом, что противоречит равенству f-g=0.

Дата добавления: 2014-01-20