
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основная теорема Алгебры
|
|
|
|
Дискриминант
Дискриминантом называется многочлен от n переменных  . Квадрат дискриминанта является симметрическим многочленом.
. Квадрат дискриминанта является симметрическим многочленом.
Лемма 2.5. Многочлен нечётной степени с вещественными коэффициентами имеет хотя бы один вещественный корень.
Доказательство. Не нарушая общности можно считать старший коэффициент многочлена равным 1. Пусть  , и
, и 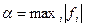 . Тогда справедливы неравенства
. Тогда справедливы неравенства 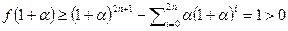 и
и  . На концах отрезка
. На концах отрезка 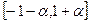 многочлен f(x) принимает значения, противоположные по знаку, следовательно, найдётся такое число
многочлен f(x) принимает значения, противоположные по знаку, следовательно, найдётся такое число , что
, что  .
.
Лемма 2.6. Многочлен второй степени с комплексными коэффициентами имеет комплексные корни.
Доказательство очевидно.
Лемма 2.7 Многочлен с вещественными коэффициентами имеет хотя бы один комплексный корень.
Доказательство. Любое натуральное число, а, значит и степень многочлена n, можно представить в виде произведения  , где m – нечётное число. Доказательство проведём методом математической индукции по s. Если s=0, то n – нечётно, и утверждение следует из приведённой выше леммы. Пусть утверждение леммы справедливо для s-1. Покажем его справедливость для s. Рассмотрим многочлен f(x) степени
, где m – нечётное число. Доказательство проведём методом математической индукции по s. Если s=0, то n – нечётно, и утверждение следует из приведённой выше леммы. Пусть утверждение леммы справедливо для s-1. Покажем его справедливость для s. Рассмотрим многочлен f(x) степени  . Построим его поле разложения. В этом поле он имеет корни
. Построим его поле разложения. В этом поле он имеет корни 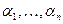 . Для некоторого вещественного числа q построим многочлен
. Для некоторого вещественного числа q построим многочлен 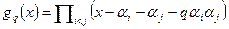 . Коэффициенты этого многочлена являются симметрическими многочленами от
. Коэффициенты этого многочлена являются симметрическими многочленами от 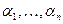 , а значит многочленами (с вещественными коэффициентами) от коэффициентов f(x). Степень
, а значит многочленами (с вещественными коэффициентами) от коэффициентов f(x). Степень  равна
равна  , и по предположению индукции многочлен
, и по предположению индукции многочлен  имеет комплексный корень. Не нарушая общности, можно считать, что найдутся различные вещественные числа
имеет комплексный корень. Не нарушая общности, можно считать, что найдутся различные вещественные числа 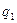 и
и  , при которых числа
, при которых числа 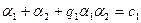 и
и - комплексные. Но тогда
- комплексные. Но тогда 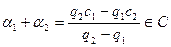 и
и 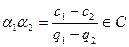 . Многочлен второй степени
. Многочлен второй степени  имеет комплексные коэффициенты, а значит и его корни
имеет комплексные коэффициенты, а значит и его корни  . Тем самым лемма доказана.
. Тем самым лемма доказана.
Теорема 2.19 (Основная теорема алгебры)
Любой многочлен над полем комплексных чисел имеет хотя бы один комплексный корень.
Доказательство. Пусть f(x) многочлен с комплексными коэффициентами 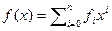 . Положим
. Положим  и
и 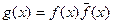 . У многочлена g(x) - вещественные коэффициенты, и по доказанному выше, g(x) имеет комплексный корень a, то есть
. У многочлена g(x) - вещественные коэффициенты, и по доказанному выше, g(x) имеет комплексный корень a, то есть 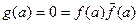 . Если f(a)=0, то теорема доказана, a – корень f(x). Пусть
. Если f(a)=0, то теорема доказана, a – корень f(x). Пусть  . По свойствам операции сопряжения
. По свойствам операции сопряжения 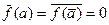 , откуда выводим
, откуда выводим  корень f(x).
корень f(x).
Следствие 2.8 Многочлен над полем комплексных чисел разлагается в произведение линейных множителей. Разложение единственно с точностью до перестановки сомножителей.
Доказательство. По основной теореме алгебры многочлен f(x) над полем комплексных чисел имеет комплексный корень a, и по теореме Безу, делится на двучлен x-a. Поделим f(x) на x-a и повторим указанные действия с частным. В результате разложим многочлен на линейные множители. Единственность разложения доказана ранее (Теорема 2.8).
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 574; Нарушение авторских прав?; Мы поможем в написании вашей работы!