Основы молекулярно-кинетической теории

Идея об атомарном строении вещества (атомистика) была высказана древнегреческим философом Демокритом (460-370 г.до н.э.). Затем она была забыта на долгие годы и вновь возродилась лишь в XVII в., получив развитие в работах М.В. Ломоносова, взгляды которого на строение вещества близки к современным. Строгое развитие молекулярной теории и формулировка основных положений молекулярно-кинетической теории (МКТ) относится к середине XIX в. (работы Р. Клаузиуса, Дж. Максвелла и Л. Больцмана). Основные положения МКТ следующие:

1. Все тела состоят из большого числа атомов и молекул. Массы атомов и молекул неорганических веществ составляют величины порядка 10^{-26 кг} , размер атомов и неорганических молекул – величины порядка 10^{-10 м} (1 Å). Органические молекулы могут состоять из сотен атомов и имеют значительно большие, по сравнению с неорганическими молекулами, размеры и массы.

В качестве единицы количества вещества используется моль – количество вещества, которое содержит столько же частиц (атомов, молекул), сколько атомов содержится в 12 граммах углерода. Было установлено, что в 12 граммах углерода содержится 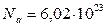атомов. Это число называется числом Авогадро. Таким образом, моль любого вещества содержит 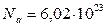атомов или молекул. Размерность числа Авогадро – моль^-1.

Масса одного моля вещества 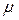называется молярной массой. Молярная масса связана с массой одной молекулы 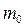соотношением 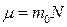и измеряется в .

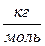Если 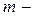масса всего вещества, то количество вещества 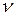(в молях) равно 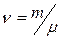. Расстояние между молекулами в веществе l можно оценить, зная плотность вещества 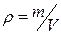(массу единицы объема) и молярную массу 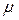. Концентрация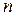

(число частиц в единице объема) связана с плотностью, молярной массой и числом Авогадро соотношением:

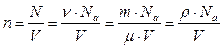, (7.3.1)

где 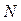- число частиц, содержащихся в веществе массой 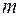; 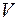- объем вещества. Величина, обратная концентрации, есть объем 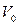, приходящийся на одну частицу.

Расстояние между частицами . (7.3.2)

Для жидкостей и твердых тел плотность слабо зависит от температуры и дав

ления, поэтому l является практически постоянной величиной порядка 10^{-10 м} и

сопоставима с размерами самих молекул.

Плотность газа сильно зависит от давления и температуры. При нормальных условиях (НУ) – давлении 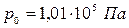, температуре 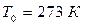– оценка дает значение 10^-9–10^{-8 м} . Таким образом, в газах расстояние между молекулами гораздо больше размеров самих молекул.

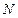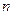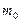Пример 7.3.1. Найти число атомов и их концентрацию в золотой монетке массой . Оценить массу и размер 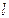атома золота. Плотность золота .

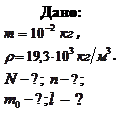
Решение:

Число атомов золота найдем по формуле 7.3.1: 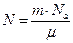, где 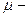молярная масса золота, которую определим по таблице Менделеева . .

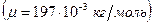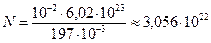Концентрация 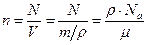, 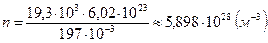. Поскольку в твердых телах атомы плотно примыкают друг к другу, размер атома 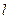примерно равен расстоянию между атомами: .

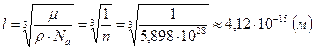Массу одной молекулы золота найдем делением его молярной массы на постоянную Авогадро: .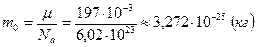

Ответ: , , , .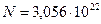

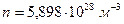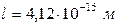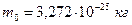2. Молекулы находятся в состоянии непрерывного теплового (скорость движения молекул определяется температурой) хаотического движения.

Движение и взаимодействие молекул подчиняется законам квантовой механики, но для широкого класса задач оказывается применимым классический подход, когда поведение молекул определяется законами классической механики Ньютона.

Двигаясь хаотически, молекулы непрерывно сталкиваются друг с другом. Путь, проходимый молекулой между двумя последовательными столкновениями, называется длиной свободного пробега . Так как молекулы движутся хаотически, имеет смысл говорить о средней длине свободного пробега .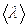

Минимальное расстояние, на которое сближаются при столкновении центры двух молекул, называется эффективным диаметром молекулы (он зависит от скорости столкновения молекул, т.е. от температуры газа).

Так как за 1 с молекула проходит путь, равный средней скорости 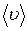, то

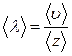, (7.3.3)

где 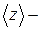среднее число столкновений, испытываемых молекулой газа за 1 с.

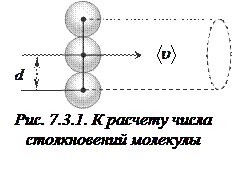
Для определения 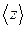представим молекулу в виде шарика диаметром 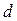. Эта молекула столкнется только с теми молекулами, центры которых будут находиться на расстояниях, равных или меньших 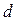, т.е. лежат внутри цилиндра радиусом 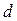(рис. 7.3.1).

Среднее число столкновений за 1 с равно числу молекул в объеме цилиндра: 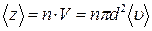, где концентрация молекул.

Расчеты показывают, что для учета движения других молекул необходимо ввести множитель :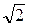

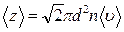. (7.3.4)

Тогда средняя длина свободного пробега равна

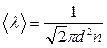, (7.3.5)

т.е. обратно пропорциональна концентрации. Величину называют площадью эффективного сечения молекул. Таким образом, .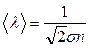

Среднее время свободного пробега 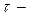время между двумя последовательными столкновениями - зависит от средней скорости молекул и длины свободного пробега:

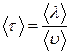. (7.3.6)

Формулы, определяющие зависимость 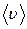от температуры газа, приводятся в параграфе 8.2.

Дата добавления: 2014-01-20