Уравнение Клапейрона–Менделеева

Между параметрами состояния идеального газа существует связь, называемая уравнением состояния. Французский инженер Б. Клапейрон (1799–1864) обобщил экспериментальные газовые законы и установил связь между параметрами (уравнение Клапейрона):

.

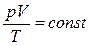Русский ученый Д.И. Менделеев (1834–1907) объединил уравнение Клапейрона с законом Авогадро. Согласно закону Авогадро, при одинаковых 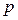и 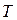моль любого газа занимает одинаковый молярный объем 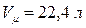, поэтому Менделеев сделал вывод, что постоянная в правой части равенства будет одинакова для всех газов. Эта общая для всех газов постоянная обозначается 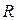и называется универсальной газовой постоянной.

Числовое значение 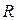можно определить, подставив в формулу 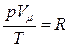значения параметров при НУ. Согласно расчетам, .

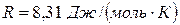Перейдем к произвольной массе газа 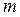. При тех же условиях она будет занимать объем 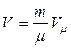. Тогда

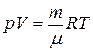. (7.4.1)

Это уравнение является уравнением состояния идеального газа (уравнением Клапейрона – Менделеева).

Введем постоянную 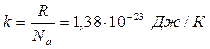, называемую постоянной Больцмана. Тогда

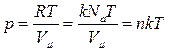, (7.4.2)

где концентрация молекул. Следовательно, из 7.4.2 следует, что давление идеального газа при данной температуре прямо пропорционально концентрации его молекул, а плотность 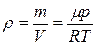обратно пропорциональна температуре.

В системе СИ давление измеряется в Паскалях . Кроме того, для измерения давления используется ряд величин:

, , .

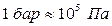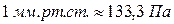Число молекул, содержащихся в 1 м³ газа при нормальных условиях, называется числом Лошмидта: .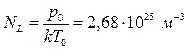

Пример 7.4.1. В баллоне объемом 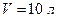находится гелий под давлением 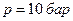и при температуре 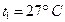. После того, как из баллона было взято 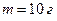гелия, температура в баллоне понизилась до 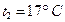. Определить давление газа, оставшегося в баллоне.

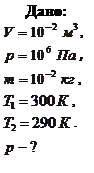
Решение:

Для начального состояния уравнение Менделеева – Клапейрона имеет вид: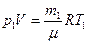. Поскольку объем гелия в конечном состоянии будет таким же (ограничен объемом сосуда), то для конечного состояния 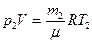. Из этих уравнений найдем массы: 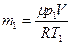и .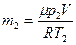

Учитывая, что 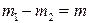, получим .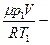

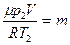Выразим искомое давление: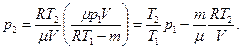

.

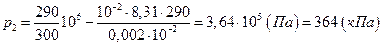Ответ: .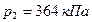

Пример 7.4.2. Найти молярную массу воздуха, считая, что он состоит (по массе) из одной части кислорода и трех частей азота.

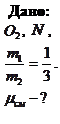Решение:

Свойствами идеального газа могут обладать не только химически однородные газы, но и газовые смеси. Чтобы применить уравнение состояния для газовой смеси, ей необходимо приписать некоторую, хотя и лишенную химического смысла, молярную массу 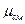. Величину 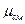выбирают такой, чтобы она удовлетворяла уравнению состояния идеального газа, записанному для смеси: 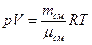. Откуда давление смеси.

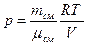Запишем уравнение Клапейрона – Менделеева для каждой из компонент смес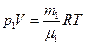и: и 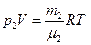. Выразим парциальные давления газов, входящих в смесь: 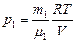и 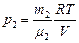. По закону Дальтона давление смеси газов равно сумме

их парциальных давлений: 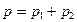. Следовательно, .

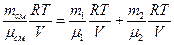Учитывая, что масса смеси 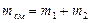, получим .

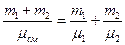Искомая молярная масса смеси равна

.

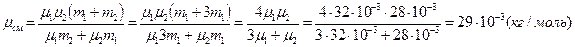Ответ: .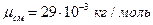

Пример 7.4.3. Плотность смеси азота и водорода при температуре 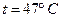и давлении 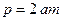равна 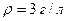. Найти концентрацию молекул азота и водорода в смеси.

Решение:

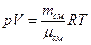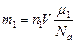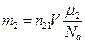Запишем уравнение состояния идеального газа для смеси газов: . Учтем, что молярная масса смеси (см. пример 7.4.2), поскольку и , то .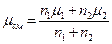

Подставим значения молярной массы смеси в уравнение Клапейрона – Менделеева.

Тогда 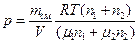или 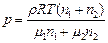(1), где 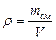– плотность смеси.

С другой стороны, давление смеси газов равно 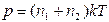(2). Решая совместно (1) и (2), найдем 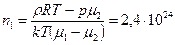(м^-3) и 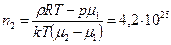(м^-3).

Ответ: , .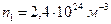

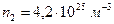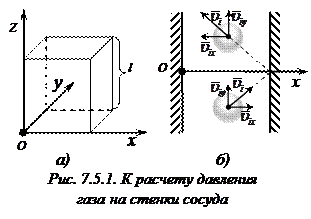7.5. Основное уравнение молекулярно-кинетической теории идеальных газов

Применим статистический метод для расчета давления газа на стенки сосуда, в котором он находится. Давление газа на любую стенку равно отношению силы, с которой молекулы газа действуют на эту стенку, к площади ее поверхности:

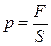. (7.5.1)

Пусть газ находится в сосуде кубической формы с ребром 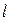(рис. 7.5.1, а). Рассмотрим стенку, перпендикулярную оси Ox (рис. 7.5.1, б). Найдем силу, с которой на нее будет действовать одна молекула газа. Обозначим 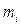массу одной молекулы, 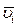скорость молекулы. Молекулы газа могут менять направление скорости только при ударе о стенки (считаем, что взаимные столкновения к этому не приводят). Изменение импульса молекулы при ударе равно 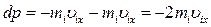. С другой стороны, изменение импульса молекулы равно импульсу силы, действующей на нее со стороны стенки. Обозначим силу, действующую на стенку сосуда со стороны молекулы 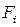. Тогда по третьему закону Ньютона сила, с которой стенка будет действовать на молекулу, равна 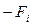. Следовательно, 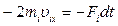, где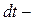

время взаимодействия молекулы со стенкой. Таким образом, сила, с которой молекула будет действовать на стенку сосуда при ударе, равна .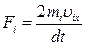

Время взаимодействия молекулы со стенкой неизвестно. Поэтому заменим кратковременно действующую ударную силу 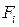эквивалентной ей средней силой 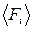так, чтобы импульс средней силы за время 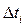между двумя последовательными ударами молекулы об одну и ту же стенку равнялся импульсу ударной силы:

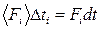. Учитывая, что 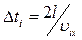(молекула возвращается, предварительно

отразившись от противоположной стенки), выразим 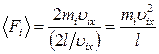. В любой

момент времени вдоль каждой координатной оси вследствие хаотичности движения перемещается 1/3 всех молекул. Средняя сила, действующая на стенку со стороны молекул газа, находящихся в сосуде, .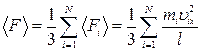

Давление, производимое газом на эту стенку:

,

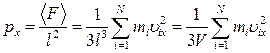где 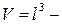объем сосуда.

Так как давление газа на все стенки сосуда одинаково (закон Паскаля), то

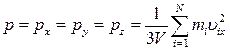. С учетом того, что 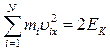, (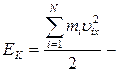суммарная кинетическая энергия молекул газа),

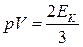. (7.5.2)

Это уравнение называется основным уравнением МКТ: произведение давления идеального газа на его объем равно двум третьим величины кинетической энергии поступательного движения всех его молекул.

Глава 8. Статистические распределения

Дата добавления: 2014-01-20