
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Энтропия и ее статистическое толкование
|
|
|
|
Как было показано выше, коэффициент полезного действия цикла Карно
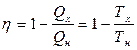 .
.
Из этого равенства следует, что
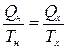 . (10.6.1)
. (10.6.1)
Отношение количества теплоты, полученного системой в изотермическом процессе, к температуре этого процесса называется приведенной теплотой. Следовательно, приведенная теплота при переходе системы из состояния 1 в состояние 3 (рис. 10.5.1) по пути 1-2-3 равна приведенной теплоте при переходе системы из состояния 1 в состояние 3 по пути 1-4-3. Это дает право утверждать, что существует некоторое физическое свойство системы, являющееся ее функцией состояния (не зависит от пути перехода в это состояние). Это свойство называется энтропией S. Оно присуще всякой термодинамической системе, а не только системе, совершающей цикл Карно.
Учитывая, что отдаваемая системой теплота отрицательна 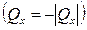 , можно записать:
, можно записать: 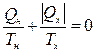 .
.
Это означает, что сумма приведенных теплот системы, совершившей круговой равновесный процесс, равна нулю.
Если считать, что тепло передается в виде отдельных порций (элементарных
порций) 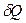 , то
, то
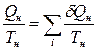 и
и 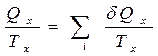 ,
,
где 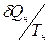 и
и  – приведенные количества тепла, переданные (или отданные) системой при температуре соответственно нагревателя
– приведенные количества тепла, переданные (или отданные) системой при температуре соответственно нагревателя 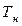 или холодильника
или холодильника 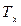 на
на
бесконечно малом участке изотермического процесса.
Строгий анализ показывает, что в любом обратимом круговом процессе
 .
.
Из равенства нулю интеграла по замкнутому контуру следует, что подынтегральное выражение  есть полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от пути, каким система пришла в это состояние. Такой функцией и является энтропия S:
есть полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от пути, каким система пришла в это состояние. Такой функцией и является энтропия S:
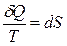 . (10.6.2)
. (10.6.2)
В результате интегрирования по всей последовательности процессов передачи тепла получим в общем виде:
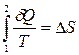 . (10.6.3)
. (10.6.3)
Следовательно, для обратимых процессов, происходящих в замкнутой системе,
изменение энтропии 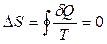 и энтропия замкнутой системы, совершившей обратимый процесс, сохраняется.
и энтропия замкнутой системы, совершившей обратимый процесс, сохраняется.
В термодинамике доказывается, что энтропия системы, совершившей необратимый процесс, возрастает: 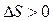 .
.
Таким образом,  , т.е. энтропия замкнутой системы может либо возрастать (необратимые процессы), либо оставаться постоянной (обратимые процессы). Это соотношение называется неравенством Клаузиуса.
, т.е. энтропия замкнутой системы может либо возрастать (необратимые процессы), либо оставаться постоянной (обратимые процессы). Это соотношение называется неравенством Клаузиуса.
Если система совершает равновесный переход из состояния 1 в состояние 2, то изменение энтропии
 .
.
Эта формула определяет энтропию с точностью до аддитивной постоянной. Физический смысл имеет не сама энтропия, а разность энтропий.
Учтем, что 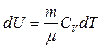 , а
, а  . Поэтому, если система совершает равновесный переход из состояния 1 в состояние 2, то
. Поэтому, если система совершает равновесный переход из состояния 1 в состояние 2, то
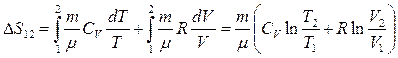 .
.
Найдем изменение энтропии идеального газа в некоторых изопроцессах.
1. Изотермический процесс  .
.
Для изотермического процесса  , следовательно
, следовательно 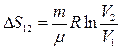 .
.
2. Изохорный процесс  . Для изохорного процесса
. Для изохорного процесса  , следовательно,
, следовательно, 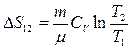 .
.
3. Адиабатический процесс 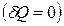 .
.
Для адиабатического процесса  и, следовательно,
и, следовательно,  . Таким образом, адиабатический процесс протекает при постоянной энтропии. Поэтому его часто называют изоэнтропийным процессом.
. Таким образом, адиабатический процесс протекает при постоянной энтропии. Поэтому его часто называют изоэнтропийным процессом.
Энтропия обладает свойством аддитивности: энтропия системы тел равна сумме энтропий тел, входящих в систему.
 Пример 10.6.1. Найти изменение энтропии при нагревании воды массой m= 500 г от t1= 00 С до t2= 1000 С с последующим превращением воды в пар той же температуры.
Пример 10.6.1. Найти изменение энтропии при нагревании воды массой m= 500 г от t1= 00 С до t2= 1000 С с последующим превращением воды в пар той же температуры.
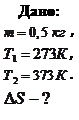
 Решение:
Решение:
Из аддитивности энтропии следует, что  , где
, где  и
и – изменения энтропии при нагревании воды и при парообразовании соответственно.
– изменения энтропии при нагревании воды и при парообразовании соответственно.
 (учли, что количество теплоты, полученное водой при нагревании,
(учли, что количество теплоты, полученное водой при нагревании, 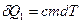 , где с=4180
, где с=4180  – удельная теплоемкость воды).
– удельная теплоемкость воды).
 (учли, что парообразование происходит при постоянной температуре Т2 и количество теплоты, полученное водой, при испарении
(учли, что парообразование происходит при постоянной температуре Т2 и количество теплоты, полученное водой, при испарении  , где r – удельная теплота парообразования воды).
, где r – удельная теплота парообразования воды).
Таким образом,  .
.
Ответ:  .
.
Пример 10.6.2. Изменение энтропии при плавлении одного моль льда составило 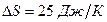 . Определить, на сколько изменится температура плавления льда при увеличении внешнего давления на
. Определить, на сколько изменится температура плавления льда при увеличении внешнего давления на 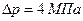 .
.
 Дано: Решение:
Дано: Решение:
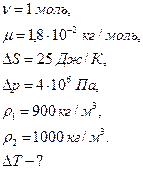 Процесс плавления льда идет при постоянной температуре, т.е.
Процесс плавления льда идет при постоянной температуре, т.е. 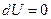 . Тогда изменение энтропии
. Тогда изменение энтропии  .
.
 При плавлении льда происходит изменение объема системы
При плавлении льда происходит изменение объема системы  , где
, где 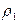 и
и  – плотности льда и воды соответственно;
– плотности льда и воды соответственно; 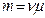 (
(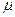 – молярная масса воды,
– молярная масса воды,  – количество молей).
– количество молей).
Температура плавления льда при давлении  была
была  , а при давлении
, а при давлении  стала
стала  .
.
Разность температур 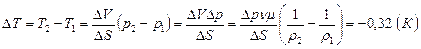 .
.
Ответ: температура понизилась на 0,32 К.
 Пример 10.6.3. Кусок меди массой
Пример 10.6.3. Кусок меди массой 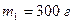 при температуре
при температуре 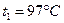 поместили в калориметр, где находится вода массой
поместили в калориметр, где находится вода массой 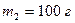 при температуре
при температуре  . Найти приращение энтропии системы к моменту выравнивания температур. Теплоемкостью калориметра пренебречь.
. Найти приращение энтропии системы к моменту выравнивания температур. Теплоемкостью калориметра пренебречь.
Дано: Решение:

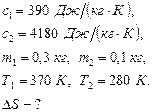 К моменту выравнивания температур приращение энтропии системы складывается из изменения энтропии воды и изменения энтропии меди (фазовые превращения не происходят). Учтем, что
К моменту выравнивания температур приращение энтропии системы складывается из изменения энтропии воды и изменения энтропии меди (фазовые превращения не происходят). Учтем, что  , где
, где 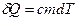 – количество теплоты, полученное при нагревании.
– количество теплоты, полученное при нагревании.
Для меди 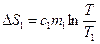 , где
, где  – удельная теплоемкость меди, Т – равновесная температура.
– удельная теплоемкость меди, Т – равновесная температура.
Для воды 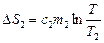 , где
, где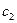 – удельная теплоемкость воды. Общее изменение энтропии после установления равновесия
– удельная теплоемкость воды. Общее изменение энтропии после установления равновесия  (1).
(1).
Из уравнения теплового баланса следует, что количество тепла, отданное куском меди, равно количеству тепла, полученному водой:  , поэтому
, поэтому 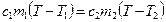 , откуда равновесная температура
, откуда равновесная температура  (2).
(2).
Подставив (2) в (1), найдем

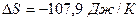
 Ответ:
Ответ:  .
.
Более глубокий смысл энтропии вскрывается в статистической физике. Неравенство Клаузиуса говорит о том, что энтропия изолированной системы не может убывать. С другой стороны, если систему предоставить самой себе, то она будет переходить из состояний менее вероятных в состояния более вероятные. Попав в наиболее вероятное состояние, система будет пребывать в нем наиболее долго. Если у нескольких состояний системы вероятность одинаково максимальная, то система будет переходить из одного максимально вероятного состояния в другое максимально вероятное состояние и обратно. Следовательно, энтропия и вероятность ведут себя сходным образом: они либо возрастают, либо остаются неизменными. Можно предположить, что между энтропией и вероятностью существует определенная связь.
 Согласно Больцману, энтропия S и термодинамическая вероятность W связаны между собой следующим образом:
Согласно Больцману, энтропия S и термодинамическая вероятность W связаны между собой следующим образом:
 ,
,
где k – постоянная Больцмана.
Термодинамическая вероятность W состояния системы – это число способов, которыми может быть реализовано данное состояние макроскопической системы, или число микросостояний, осуществляющих данное макросостояние (статистический вес данного макросостояния). Термодинамическая вероятность W> 1, в отличие от математической вероятности, которая меньше или равна 1.
Рассмотрим систему, состоящую из 4 молекул (пронумерованных), находящихся в сосуде. Мысленно разделим сосуд пополам. Рассмотрим различные состояния, отличающиеся друг от друга числом молекул в верхней и нижней половинах сосуда (рис. 10.6.1).
Вероятность того, что все молекулы соберутся с одной половине сосуда, равна
 .
.
При увеличении числа молекул до 10 вероятность того, что все молекулы соберутся в одной половине сосуда, уменьшается до 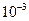 .
.
В реальных газах концентрация молекул приближается к 1024 м-3, поэтому вероятность того, что молекулы соберутся в одной половине сосуда, стремится к 0. Рассмотрим обратную ситуацию. Пусть газ находится в одной половине сосуда. Уберем перегородку. Газ распространится на весь сосуд. Возможен ли обратный процесс? Да, но вероятность этого события близка к нулю. Следовательно, необратимый процесс – это процесс, обратный которому маловероятен.
Таким образом, энтропия может рассматриваться как мера вероятности состояния термодинамической системы. Формула Больцмана позволяет дать энтропии следующее статистическое толкование: энтропия является мерой неупорядоченности системы (чем больше число микросостояний, реализующих данное макросостояние, тем больше энтропия). В состоянии равновесия – наиболее вероятного состояния системы – число микросостояний максимально, при этом максимальна и энтропия.
|
|
|
Дата добавления: 2014-01-20; Просмотров: 1492; Нарушение авторских прав?; Мы поможем в написании вашей работы!