Смачивание

Проявление поверхностного натяжения можно обнаружить, наблюдая явления, происходящие на границе раздела твердого тела с жидкостью.

Если при соприкосновении жидкости с твердым телом взаимодействие между их молекулами сильнее, чем взаимодействие между молекулами в самой жидкости, то жидкость стремится увеличить поверхность соприкосновения и растечется по твердому телу. В этом случае говорят, что жидкость смачивает твердое тело (вода на стекле, ртуть на железе). Если взаимодействие между молекулами твердого тела и молекулами жидкости слабее, чем между молекулами самой жидкости, то жидкость будет стремиться сократить поверхность соприкосновения с твердым телом. В этом случае говорят, что жидкость не смачивает твердое тело (вода на парафине, ртуть на стекле).

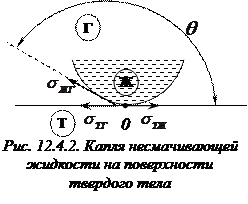Рассмотрим каплю жидкости на поверхности твердого тела. Форма капли устанавливается под влиянием трех сред: жидкости Ж, твердого тела Т, воздуха или газа Г. Эти три среды имеют общую границу – окружность, ограничивающую каплю. К линии соприкосновения трех сред приложены три силы поверхностного натяжения, которые направлены по касательной внутрь поверхности соприкосновения соответствующих двух сред. Покажем их направление в точке О – точке пересечения линии соприкосновения трех сред с плоскостью чертежа (рис. 12.4.1 и 12.4.2).

Эти силы, отнесенные к единице длины линии соприкосновения, равны соответствующим поверхностным натяжениям. Угол 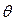между касательными к поверхности жидкости и твердого тела называют краевым углом. Условием равновесия капли (рис. 12.4.1) является равенство нулю проекций сил поверхностного натяжения на направление касательной к поверхности твердого тела:

,

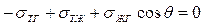откуда .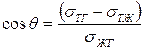

Из этого равенства вытекает, что краевой угол может быть острым или тупым в зависимости от значени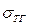й и 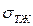. Если 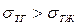, то 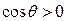и угол 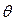– острый, т.е. жидкость смачивает твердую поверхность. Если 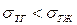, то 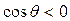и угол 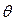– тупой, т.е. жидкость не смачивает твердую поверхность.

Краевой угол должен удовлетворять условию

.

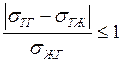Если это условие не выполняется, то капля жидкости ни при каких условиях не может находиться в равновесии. Если 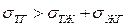, то жидкость растекается по поверхности твердого тела, покрывая его тонкой пленкой (керосин на поверхности стекла), – имеет место полное смачивание. Если 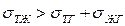, то жидкость стягивается в шаровую каплю (роса на поверхности листа дерева).

12.5. Капиллярные явления

Поверхность смачивающей жидкости, находящейся в узкой трубочке (капилляре), принимает вогнутую форму, а не смачивающей – выпуклую. Такие изогнутые поверхности жидкости называются менисками. Пусть капилляр в виде цилиндрической трубки с радиусом канала r погружен одним концом в смачивающую его стенки жидкость (рис. 12.5.1). Мениск в нем будет иметь сферическую форму (R – радиус сферы). Под мениском давление жидкости будет на 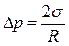меньше, чем в широком сосуде, где поверхность жидкости практически плоская. Поэтому в капилляре жидкость поднимается на высоту h, при которой вес столба жидкости в нем уравновесит отрицательное дополнительное давление:

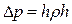, (12.5.1)

где 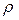– плотность жидкости. Учитывая, что 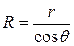, получим

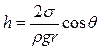. (12.5.2)

Таким образом, высота поднятия смачивающей жидкости в капилляре тем больше, чем меньше его радиус. Эта же формула позволяет определить и глубину опускания в капилляре несмачивающей жидкости.

Пример 12.5.1. В воду опущена стеклянная трубка с диаметром внутреннего канала, равным 1 мм. Найти массу воды, вошедшей в трубку.

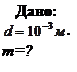Решение:

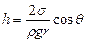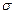Высота поднятия смачивающей жидкости в капилляре определяется по формуле: , где – поверхностное натяжение воды, 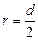– радиус капилляра, 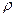– плотность воды. Считая поверхность воды плоской, то есть пренебрегая явлением смачивания (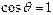), получим .

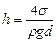Учитывая, что масса воды 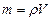, где объем воды в капилляре 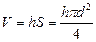, получим 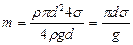. Находим по таблице 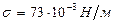и подставляем в формулу

числовые значения: .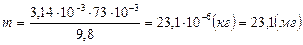

Ответ: .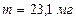

Дата добавления: 2014-01-20