Давление под искривленной поверхностью жидкости

Формула Лапласа

Если поверхность жидкости не плоская, а искривленная, то она оказывает на жидкость избыточное (дополнительное) давление . Это давление, обусловленное силами поверхностного натяжения, для выпуклой поверхности положительно (рис. 12.3.1, а), а для вогнутой – отрицательно (рис. 12.3.1, б).

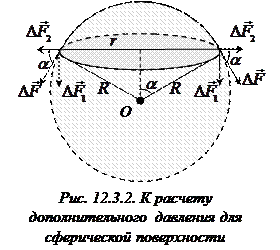Вычислим дополнительное давление для сферической поверхности радиусом R. Мысленно отсечем от нее шаровой сегмент, опирающийся на окружность радиуса 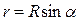(рис. 12.3.2). На каждый элемент длины 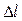этой окружности в направлении, касательном к поверхности сегмента, действует силы поверхностного натяжения, численно равная .

Разложим вектор , направленный по касательной к поверхности, на составляющие и 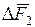. Геометрическая сумма составляющих 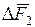для всего периметра окружности, ограничивающей рассматриваемый сегмент, будет равна нулю, т.к. силы на противоположных сторонах контура направлены в противоположные стороны и взаимно уравновешивают друг друга. Составляющие 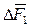в сумме дадут равнодействующую, направленную по нормали к плоскости сечения и численно равную

. (12.3.1)

Равнодействующая сил поверхностного натяжения будет прижимать рассматриваемый сегмент к остальной части жидкости по всей разделяющей их поверхности 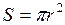. Следовательно, дополнительное давление внутри жидкости, обусловленное кривизной ее поверхности, равно

(12.3.2)

Если поверхность жидкости вогнутая, то аналогично можно доказать, что

. (12.3.3)

В общем случае, избыточное давление под произвольной поверхностью жидкости двоякой кривизны можно описать формулой Лапласа:

, (12.3.4)

где R₁ и R₂ – радиусы кривизны двух любых взаимно перпендикулярных нормальных сечений поверхности жидкости в данной точке.

Для сферической поверхности (R₁=R₂=R) , что соответствует полученной ранее формуле.

Для плоской поверхности (R₁=R₂=) .

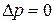Пример 12.3.1. Какую работу против сил поверхностного натяжения надо совершить, чтобы выдуть мыльный пузырь радиусом 0,05 м? Чему равно добавочное давление внутри пузыря?

Решение:

Мыльный пузырь представляет собой очень тонкую пленку мыльной воды приблизительно сферической формы. Эта пленка имеет две поверхности – наружную и внутреннюю. Пренебрегая толщиной пленки и считая радиусы обеих сфер одинаковыми, найдем их общую площадь: .

Т.к. до образования пузыря поверхность мыльной воды, из которой он выдут, была очень мала, можно считать, что получили приращение площади поверхности мыльной воды. Но изменение поверхностной энергии связано с увеличением поверхности как . Совершаемая при выдувании пузыря работа против сил поверхностного натяжения идет на увеличение поверхностной энергии: .

Для определения избыточного давления внутри пузыря учтем, что каждая из сферических поверхностей пузыря – наружная и внутренняя – производит вследствие своей кривизны давление на воздух внутри пузыря. Это давление найдем по формуле Лапласа, считая :. По таблице .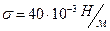

Следовательно,, .

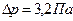Ответ: , .

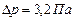Дата добавления: 2014-01-20