Преобразований Лапласа

Решение линейных дифференциальных уравнений с помощью

Идея метода в том, что решение диф. уравнения из области функции действительного переменного f(t), переносится в область комплексного переменного.

Р = a +j*ω (область комплекс переменного)

где α- вещественная часть комплексного переменного;

j *ω— мнимая часть комплексного числа.

J означает корень из минус 1, где операции решения принимает более простой вид. Вместе диф. уравнение решается алгебраически.

Полученное операторное решение переводится обратно в область действительного переменного.

Формально символ дифференцирования d/ dt заменяется оператором р.

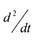соответственно ---- + р²и т.д.

Символ интегрирования ƒdt заменяется 1/Р.

Функция времени f(t) соответственно преобразуется, называется оригиналом, а функция f(p), полученная в результате преобразования - изображение.

Символ р - называют оператором, форму записи уравнения -операторной.

Функция f(p) получается умножением f(t) на экспоненциальную

функцию е

F(p) = ƒf(t)*e^-pt*αt

Пример: 1) Найти изображение функции времени f(t) = е ^–pt Напишем выражение преобразования функции Лапласа и проинтегрируем:

F(p) = ƒf(t) *e^-pt *t = -l/(α+p) *e^-(α+p)t ₌ 1/(α+p)

2) оригинал функции имеет вид

Onput < О

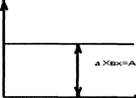
Δ лвых= ----------

Anput > О

Изменение входной величины элемента или системы имеет

скачкообразный характер.

Для нахождения по оригинальной функции соответствующих изображений и по изображениям оригиналов существуют специальные таблицы преобразования Лапласа.

F(t) оригинал	F(p) изображение
{1}	1/Р
А{1}	А/Р
t	1/p^2
t^2	2/р^4
t^n/n	1/ P^m+1
е^±^2t	/Р±а

sinαt	1/ /(P^2 +a^2)
соsαt	P/(P^2+a^2)
t∙e^-αt	1/(py+α)y^2y
t* sinat	α/(P + a)^2+a2
t*cosat	P+α/(P + a)^2+a2

Динамическими звеньями являются: переходная функция, передаточные функции и частично передаточная функция или частные характеристики.

Переходной функцией Хвых(х) называют изменения выходной величины во времени, вызванное единичным скачкообразным изменением входной величины Хвх = 1.

Переходную функцию получают постановкой диф. уравнения или уравнения в операторной форме переходного процесса Хвх =1.

Для диф уравнения

T*dХХвы/dt₊ТХХвы=КХвх

Предположим что Хвх = 1, то получим

dXXвы

Т + ТХХвы = К

dt

Но режим этого уравнения относительно Хвых, найдем по Лапласу его

изображение:

Тррхвы + ТХХвы = К

Хвых = К/Т((+1) переходная функция для диф. уравнения

Графически изображение переходных функций зависит от динамических свойств звена и характера внесенных воздействий, и имеет вид аналогичных переходным процессам только с уменьшением ординате в Хвх раз.

Передаточной функций w(p) звена или системы называют отношение изображения по Лапласу выходной величины к отношению изображения

входной величины при нулевых начальных условиях.

Передаточная функция из диф уравнения звена или системы записанной в операторной форме.

Так для диф уравнения

Т* dХХвы/dt+XХвх

Найдем изображение функции по Лапласу

Хвых(Тр + 1) = КХвх

Разделим обе части на Хвх и решим относительно Vbx/Xbx:

Хвых/Хвх = К/Т_p-1 =W(p)

Передаточная функция

Частотой характеристикой называют функцию частоты, описывающей изменение амплитуды и фазы гармонических колебаний выходной величины элемента. Частотные характеристики отличаются от функции входного воздействия только по амплитуде и фазе.

Дата добавления: 2014-01-20