Типовые звенья САР и их характеристики

О

Частотные характеристики САР

Их понятие следует из преобразований Фурье, являющегося частным случаем преобразования Лапласа. Аналогично ему преобразование Фурье представляет собой функциональное преобразование

F(jw)=∫f(t)e-^JWt,dt

Заметим, что частотная характеристика получается из изображения функции по Лапласу, в котором Р заменяют на jco. Например, изображение по Фурье функции

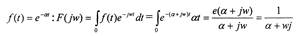
Если на выход звена подать сигнал Хвх = Авх * sin ωt, то по окончании переходного процесса в звене на его выходе установится тот же гармонич сигнал, но с амплитудой Авх = ΔХ2 и отставание его по фазе на угол ср.

Хвх=Авых* sin(wt+φ)

Хвх

Зависимость отклонения амплитуды гармонических колебаний на выходе системы или звена к амплитуде колебаний на его выходе от частоты называется амплитудно-частотной характеристикой (АЧХ).

A(w) = Авых / Авх

Зависимость разности фаз выходных входных гармоничных колебаний называется фазо-частотной характеристикой (ФЧХ).

φ(w) = φ вых - φ вх

Отношение выходного гармоничного сигнала звена или системы к входному гармоническому сигналу, выраженная в комплексной форме называется амплитудно-фазовой характеристикой (АФХ) или частотной передаточной функцией.

АФХ объединяет АЧХ и ФЧХ и является комплексной функцией частоты и как видное комплексное число м.б. представлено в 3-х формах записи:

1) в виде суммы вещественной и мнимой частей

W(jω) = Re(ω)+jJm(ω)

2) в тригонометрической форме

W (jω) = А(ω) * [cos(φ (ω) + jsin(φ(ω)]

3) в показательной форме

W(jω) = A*ω*e^jф(ω) Т.к, согласно теореме Эйлера:

cos(ω) +jsin(φ(ω)) = e^jф(ω) приведенных формулах А(ω) - модуль,φ(ω) - фаза

причем:

Пример

Построить АФХ системы, описываемой дифф. уравнениями:

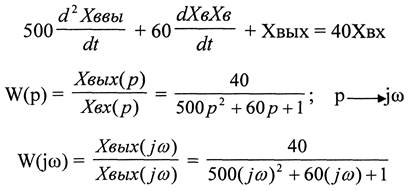
Преобразуем с учетом того, что J² = - 1

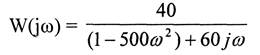
Избавимся от мнимости в знаменателе, умножив его на сопряженное

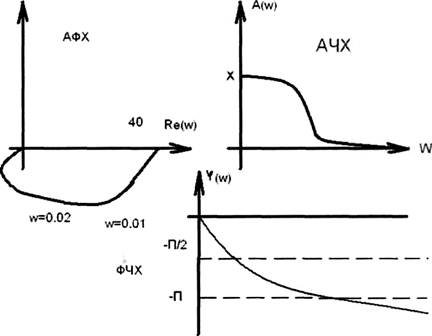
Подставляя в Re и Jm значения ω от 0 до °°, находим координаты точек на комплексной плоскости, кот являются концами векторов, проведенных из начало координат, соединяя эти концы векторов плавной

кривой, получили АФХ.

w 0 0.01 0.02 0.03

Re(w) 40 30 +16 +6

Im(w) 0 -19 -24 -20

0.04 0.05 0.06

+4 -1.1 -2.3

-16.7 -13.3 -10

График АФХ строится по известным АЧХ и ФЧХ:

lm(w)

*■*• W

Различают 5 основных типов звеньев:

1) усилительные;

2) апериодические;

3) колебательные;

4) дифференцирующее;

5) интегрирующее.

Дата добавления: 2014-01-20