Требования к достоверности контрольной и управляющей информации согласно ГОСТ 26.205-83

Вероятностные характеристики	Вероятность события Р, не более
Категории систем
Вероятность трансформации команды ТУ	10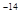	10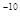	10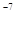
Вероятность трансформации сообщений ТС и ТИ	10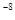	10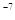	10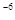
Вероятность трансформации знака буквенно-цифровой информации или отсчёта кодового ТИ	10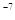	10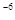	10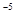
Вероятность отказа от исполнения посланной команды (с повторением передачи до пяти раз)	10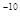	10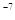	10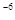
Вероятность потери контрольной информации при спорадической передаче (с повторениемпередачи до пяти раз)	10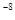	10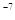	10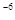
Вероятность потери команды	10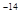	10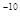	10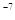
Вероятность образования ложной команды или контрольного сообщения	10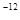	10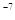	10

По величине показателя достоверности, которым служит вероятность искажения различных типов сообщений, системы телемеханики разделяются на три категории, причём наибольшие требования предъявляются к телемеханическим системам первой категории, наименьшие – к системам третьей категории.

Характеристики табл. 7.1 используются при проектировании телемеханических систем.

7.5. ПОМЕХОУСТОЙЧИВОСТЬ ПЕРЕДАЧИ КОДОВЫХ КОМБИНАЦИЙ ПРИ НЕЗАВИСИМЫХ ОШИБКАХ

Расчет помехоустойчивости передачи различных кодовых комбинаций является большой и самостоятельной темой. Рассмотрим лишь расчет трансформаций, т.е. перехода одной кодовой комбинации в другую [6].

Расчет вероятности трансформаций для несимметричного канала с независимыми ошибками. В этом случае при расчетах можно придерживаться положений, вытекающих из теорем теории вероятностей.

Теорема первая. Если в двоичном канале заданы вероятности двух переходов, то вероятности двух других переходов могут быть найдены на основе теоремы о полной группе событий;

Теорема вторая. Вероятность того, что одна кодовая комбинация перейдет в другую, равна произведению вероятностей переходов ошибок каждого символа.

Например, передана комбинация 11011. Вероятность того, что под воздействием помех эта комбинация исказится и вместо нее будет принята, на­пример, комбинация 10101, рассчитывают таким образом. В старшем (пятом) и в первом (младшем) разрядах единицы приняты правильно: (1®1) и (1®1). В четвертом и во втором разрядах единицы подавлены помехами и трансформировались в нули, т.е. 1®0 и 1®0. В третьем разряде 0 перешёл в 1, т.е. 0®1. В результате получаем вероятность перехода комбинации 11011 в комбинацию 10101:

Р (11011®10101) = P₁₁P₁₀P₀₁P₁₀P₁₁.

Если необходимо находить вероятности возникновения обнаруженных и необнаруженных ошибок или нескольких ошибок при передаче сообщения, то пользуются указанными теоремами.

Дата добавления: 2014-01-20