Вероятность гипотез. Формулы Бейеса

Следствием формулы (3.6) является формула Байеса или теорема гипотез. Она позволяет переоценить вероятности гипотез H_i, принятых до опыта и называемых априорными («a priory», доопытные, лат.) по результатам уже проведенного опыта, то есть найти условные вероятности P (H_i | A), которые называются апостериорными («a posteriori», послеопытные, лат.).

Пусть событие А может наступить при условии появления одного из несовместных событий Н ₁, Н ₂,…, Н_n, образующих полную группу. Поскольку заранее не известно, какое из этих событий наступит, их называют гипотезами. Вероятность появления события А определяется по формуле полной вероятности (3.6):

Р (А) = .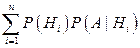

Допустим, что произведено испытание, в результате которого появилось событие А. Поставим своей задачей определить, как изменились (в связи с тем, что событие А уже наступило) вероятности гипотез. Другими словами, будем искать условные вероятности

P (H ₁| A), P (H ₂| A),…, P (H_n | A).

Найдем сначала условную вероятность P (H ₁| A). По теореме умножения имеем

Р (AH ₁) = Р (А) P (H ₁| A) = P (H ₁) P (А / H ₁).

Отсюда

.

Заменив здесь Р (А) по формуле (3.6), получим

.

Аналогично выводятся формулы, определяющие условные вероятности остальных гипотез, т.е. условная вероятность любой гипотезы H_i (i = 1,2,..., n) может быть вычислена по формуле

(3.8)

Полученные формулы называют формулами Бейеса (по имени английского математика, который их вывел; опубликованы в 1764 г.). Формулы Бейеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.

Теорема. Вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, деленному на полную вероятность этого события.

Замечание. Вероятности P (H ₁), …, P (H_n) часто называют априорными вероятностями группы событий H ₁, …, H_n, в то время как условные вероятности P (H ₁| A),…, P (H_n | A) – апостериорными, полученными после дополнительного эксперимента, в котором произошло событие А. В связи с этим формула Байеса называется также формулой обновления априорных вероятностей.

Приведем несколько задач, решаемых с помощью полученных формул условной вероятности.

Статистический контроль качества. Формула Байеса играет большую роль в планировании процедур гарантийного контроля качества выпускаемой продукции. Производитель продукта должен выполнять определенные договорные обязательства перед потребителем, которые, так или иначе, сводятся к ограничениям на долю некондиционной продукции, поставляемой потребителю, или, что то же, доля кодндиционной продукции должна быть достаточно высокой. Обеспечение этих ограничений достигается с помощью контроля (как правило, выборочног) производимой продукции. Пусть Q_in – доля кондиционной продукции среди изготавливаемой предариятием. Обычно эта доля называется входным уровнем качества, и необходимость контроля продукции обуславливается невысоким значеним Q_in, которое не удовлетворяет потребителя. Если контроль продукции производится на основе обследования только ее части (так называемый выборочный или статистический контроль качества), то возникает вероятность принятия ошибочного решения о качестве контролируемого продукта: с некоторой вероятностью b процедура контроля может пропустить некондиционный продукт или, наоборот, с вероятностью a отклонить кондиционный. Вероятность b называется риском потребителя, а вероятность a – риском изготовителя. Существуют методы расчета этих рисков на основе вероятностной модели статистического контроля. Зная значения Q_in, a и b, можно, используя формулу Байеса, вычислить выходной уровень качества Q_out – долю кондиционной продукции, срели отсылаемой потребителю после контроля.

Пусть H ₁ – событие, состоящее в том, что поступивший на контроль продукт кондиционен, а H ₂ – продукт «плохой». В наших обозначениях Р (H ₁) = Q_in. Пусть, далее, А – утверждение о кондиционности продукта после его контроля. Тогда Q_out = P (H ₁/ А) – вероятность кондиционности продукта при условии, что он проше контроль. Наконец, P (А / H ₁) = 1 – a и P (А / H ₂) = b. По формуле Байеса

.

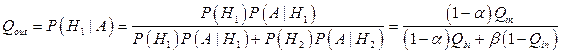Проиллюстрируем расчеты, производимые по этой формуле, на основе конкретных числовых данных. Пусть предприятие работает из рку вон плохо: Q_in = 0,1 (90% выпускаемой продукции не удовлетворяет нормам качества), но на предприятии существует довольно жесткий контроль, в котором риск потребителя b = 0,01, а риск изготовителя a = 0,1. Тогда выходной уровень качества

,

и это совсем неплохо по сравнению с тем, что было до контроля.

Пример. Детали, изготовляемые цехом завода, попадают для проверки их на стандартность к одному из двух контролеров. Вероятность того, что деталь попадает к первому контролеру, равна 0,6, а ко второму – 0,4. Вероятность того, что годная деталь будет признана стандартной первым контролером, равна 0,94, а вторым – 0,98. Годная деталь при проверке была признана стандартной. Найти вероятность того, что эту деталь проверил первый контролер.

Решение. Обозначим через А событие, состоящее в том, что годная деталь признана стандартной. Можно сделать два предположения:

1) деталь проверил первый контролер (гипотеза H ₁);

2) деталь проверил второй контролер (гипотеза H ₂).

Искомую вероятность того, что деталь проверил первый контролер, найдем по формуле Бейеса:

По условию задачи имеем:

Р (H ₁) = 0,6 (вероятность того, что деталь попадает к первому контролеру);

Р (H ₂) = 0,4 (вероятность того, что деталь попадет ко второму контролеру);

P (А / H ₁) = 0,94 (вероятность того, что годная деталь будет признана первым контролером стандартной);

P (А / H ₂) = 0,98 (вероятность того, что годная деталь будет признана вторым контролером стандартной).

Искомая вероятность

.

Как видно, до испытания вероятность гипотезы H ₁ равнялась 0,6, а после того, как стал известен результат испытания, вероятность этой гипотезы (точнее, условная вероятность) изменилась и стала равной 0,59. Таким образом, использование формулы Бейеса позволило переоценить вероятность рассматриваемой гипотезы.

Дата добавления: 2014-01-20