Формула Бернулли

ПОВТОРЕНИЕ ИСПЫТАНИЙ

Если производится некоторое количество испытаний, в результате которых может произойти или не произойти событие А, и вероятность появления этого события в каждом из испытаний не зависит от результатов остальных испытаний, то такие испытания называются независимыми относительно событияА.

Примерами независимых испытаний могут служить: несколько (n раз) подбрасываний монеты: стрельба (n раз) по мишени без поправок на ранее допущенную ошибку при новом выстреле; несколько (n раз) выниманий из урны одинаковых на ощупь занумерованных шаров, если шары каждый раз (после просмотра) возвращаются в урну, и т.д.

В разных независимых испытаниях событие А может иметь либо различные вероятности, либо одну и ту же вероятность. Будем далее рассматривать лишь такие независимые испытания, в которых событие А имеет одну и ту же вероятность.

При практическом применении теории веоятностей часто используется стандартная схема, называемая схемой Бернулли или схемой независимых испытаний.

Определение. Последовательность n независмых испытаний, в каждом из котрых может произойти некоторое событие А (его называют успехом) с вероятностью Р (А) = р или противоположное ему событие 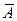(его называют неудачей) с вероятностью 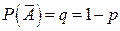, называется схемой Бернулли.

Часто успеху сопоставляют число 1, неудчае – число 0. Элементарным событием для n опытов будет последовательность из n нулей и единиц. Например, тройка чисел (0, 1, 0) означает, что событие А наступило во 2-м опыте, а в 1-м и 3-м – не наступило.

Ниже воспользуемся понятием сложного события, понимая под ним совмещение нескольких отдельных событий, которые называют простыми.

Простейшая задача, относящаяся к схеме Бернулли, состоит в определении вероятности того, что в n независмых испытанях событие А наступит m раз (0 £ m £ n) и, следовательно, не осуществится n – m раз. Важно подчеркнуть, что не требуется, чтобы событие А повторилось ровно m раз в определенной последовательности. Например, если речь идет о появлении события А три раза в четырех испытаниях, то возможны следующие сложные события: . Запись означает, что в первом, втором и третьем испытаниях событие А наступило, а в четвертом испытании оно не появилось, т.е. наступило противоположное событие 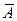; соответственный смысл имеют и другие записи.

Искомую вероятность обозначают Р_n (m) или P_n,m или P (m _n = m), где m _n – число появления события А в серии из n опытов. Например, символ Р ₅(3) означает вероятность того, что в пяти испытаниях событие появится ровно 3 раза и, следовательно, не наступит 2 раза.

Эту вероятность в принципе можно посчитать, используя теоремы сложения и умножения вероятностей, как это делалось в рассмотренных выше примерах. Однако, при достаточно большом количестве испытаний это приводит к очень большим вычислениям. Таким образом, возникает необходимость разработать общий подход к решению поставленной задачи. Этот подход реализован в формуле Бернулли. (Якоб Бернулли (1654 – 1705) – швейцарский математик).

Вывод формулы Бернулли. Вероятность одного сложного события, состоящего в том, что в n испытаниях событие А наступит m раз и не наступит n – m раз, по теореме умножения вероятностей независимых событий равна p^mq^n–m. Таких сложных событий может быть столько, сколько можно составить сочетаний из n элементов по m элементов, т.е. 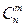. Так как эти сложные события несовместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равна сумме вероятностей всех возможных сложных событий. Поскольку же вероятности всех этих сложных событий одинаковы, то искомая вероятность (появления m раз события А в n испытаниях) равна вероятности одного сложного события, умноженной на их число:

или

. (4.1)

Полученную формулу называют формулой Бернулли.

Теорема. Если призводится n независимых испытаний, в каждом из которых вероятность появления события А равна р, а вероятность его непоявления равна q = 1 – p, то вероятность того, что событие А произойдет m раз определеяется формулой Бернулли

, m = 0, 1, 2, …, n.

Доказательство. Вероятность одного сложного события, состоящего в том, что событие А в n независиымх опытах появится m раз в первых m опытах и не появится (n – m) раз в остальных опытах (это событие 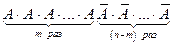) по теореме умножения вероятностей равна p^mq^n–m. Вероятность появления события А снова m раз, но в другом порядке (например, 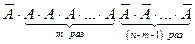или и т.д.) будет той же самой p^mq^n–m.

Число таких сложных событий – в n опытах m раз встречается событие А в различном порядке – равно числу сочетаний из n элементов по m элементов, т.е. 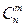. Так как все эти сложные события несовместны, то по теореме сложения вероятностей искомая вероятность равна сумме вероятностей всех возможных сложных событий, то есть

.

Можно заметить, что вероятности являются коэффициентами при x^m в разложении (q + px) ⁿ по формуле бинома Ньютона:

.

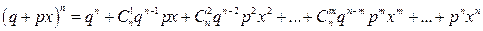Поэтому совокупность вероятностей Р_n (m) называют биномиальным законом распределения вероятностей, а функцию j(х) = (q + px) ⁿ – производящей функцией для последовательности независимых опытов.

Если в каждом из независимых испытаний вероятности наступления события А разные, то вероятность того, что событие А наступит m раз в n опытах, равна коэффициенту при m -й степени многочлена j_n (z) = (q ₁ + p ₁ z)(q ₂ + p ₂ z)× …×(q_n + p_nz), где j_n (z) – производящая функция.

Если в серии из n независимых опытов, в каждом из которых может произойти одно и только одно из k событий А ₁, А ₂, …, A_k с соответствующими вероятностями р ₁, р ₂, …, р_k, то вероятность того, что в этих опытах событие А ₁ появится m ₁ раз, событие А ₂ – m ₂ раз,…, событие А_k – m_k раз, равна

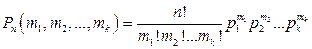, (4.2)

где . Вероятности (4.2) называются полиномиальным распределением.

Формула Бернулли важна тем, что справедлива для любого количества независимых испытаний, т.е. того самого случая, в котором наиболее четко проявляются законы теории вероятностей.

Пример. Вероятность того, что расход электроэнергии в продолжение одних суток не превысит установленной нормы, равна р = 0,75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.

Решение. Вероятность нормального расхода электроэнергии в продолжение каждых из 6 суток постоянна и равна р = 0,75. Следовательно, вероятность перерасхода электроэнергии в каждые сутки также постоянна и равна q =1 – р =1 – 0,75 = 0,25.

Искомая вероятность по формуле Бернулли равна

.

Пример. Производится 3 независимых выстрела по цели. Вероятности попадания при разных выстрелах одинаковы и равны р = 0,9. Какова вероятность: а) промаха; б) одного попадания; в) двух попаданий; г) трех попаданий? Решить задачу в случае, если вероятности попадания при разных выстрелах различны: р ₁ = 0,7, р ₂ = 0,8, р ₃ = 0,9.

Решение. В данном случае n = 3, p = 0,9, q = 0,1. Пользуясь формулой Бернулли (4.1), находим:

а) 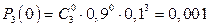– вероятность трех промахов;

б) – вероятность одного попадания;

в) – вероятность двух попаданий;

г) 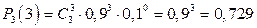– вероятность трех попаданий.

Эти результаты можно изобразить графически, отложив по оси Ох значения m, на оси Oy – значения P_n (m) (рис. 4.1).

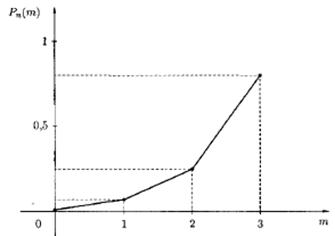
Рис. 4.1

Ломаная, соединяющая точки (0; 0,001), (1; 0,027), (2; 0,243), (3; 0,729), называется многоугольником распределения вероятностей.

Если вероятности при разных выстрелах различны, то производящая функции имеет вид j ₃(z) = (0,3 + 0,7 z)(0,2 + 0,8 z)(0,1 + 0,9 z) = 0,504 z ³ +0,398 z ² +0,092 z + 0,006. Откуда находим вероятность трех, двух, одного попаданий, промаха соответственно: Р ₃(3) = 0,504, Р ₃(2) = 0,398, Р ₃(1) = 0,092, Р ₃(0) = 0,006. (Контроль: 0,504 + 0,398 + 0,092 + 0,006 = 1).

Дата добавления: 2014-01-20