Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях

Вновь будем считать, что производится n независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна р (0 < р < 1). Поставим перед собой задачу найти вероятность того, что отклонение относительной частоты m / n от постоянной вероятности р по абсолютной величине не превышает заданного числа e > 0. Другими словами, найдем вероятность осуществления неравенства

. (4.15)

Эту вероятность будем обозначать так: Р (| m/n – р | £ e). Заменим неравенство (4.15) ему равносильными:

или .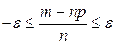

Умножая эти неравенства на положительный множитель , получим неравенства, равносильные исходному:

.

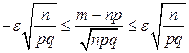Воспользуемся интегральной теоремой Лапласа в форме (4.14). Положив 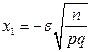и , имеем

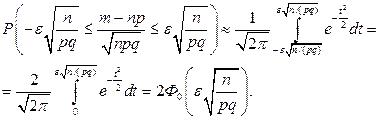
Наконец, заменив неравенства, заключенные в скобках, равносильным им исходным неравенством, окончательно получим

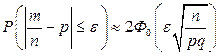. (4.16)

Итак, вероятность осуществления неравенства приближенно равна значению удвоенной функции Лапласа 2Ф₀(х) при .

Пример. Вероятность того, что деталь не стандартна, р = 0,1. Найти вероятность того, что среди случайно отобранных 400 деталей относительная частота появления нестандартных деталей отклонится от вероятности р = 0,1 по абсолютной величине не более чем на 0,03.

Решение. По условию, n = 400; p = 0,1; q = 0,9; e = 0,03. Требуется найти вероятность Р (m /400 – 0,1| £ 0,03). Пользуясь формулой (4.16), имеем

.

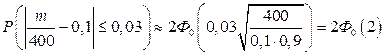По таблице приложения находим Ф₀(2) = 0,4772. Следовательно, 2Ф₀(2) = 0,9544. Итак, искомая вероятность приближенно равна 0,9544.

Смысл полученного результата таков: если взять достаточно большое число проб по 400 деталей в каждой, то примерно в 95,44% этих проб отклонение относительной частоты от постоянной вероятности р = 0,1 по абсолютной величине не превысит 0,03.

Пример. Вероятность того, что деталь не стандартна, р = 0,1. Найти, сколько деталей надо отобрать, чтобы с вероятностью, равной 0,9544, можно было утверждать, что относительная частота появления нестандартных деталей (среди отобранных) отклонится от постоянной вероятности р по абсолютной величине не более чем на 0,03.

Решение. По условию, p = 0,1; q = 0,9; e = 0,03; Р (m / n – 0,1| £ 0,03) = 0,9544. Требуется найти n.

Воспользуемся формулой (4.16). В силу условия

.

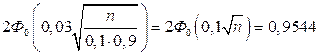Следовательно, . По таблице приложения находим Ф₀(2) = 0,4772. Для отыскания числа n получаем уравнение . Отсюда искомое число деталей n = 400.

Смысл полученного результата таков: если взять достаточно большое число проб по 400 деталей, то в 95,44% этих проб относительная частота появления нестандартных деталей будет отличаться от постоянной вероятности р = 0,1 по абсолютной величине не более чем на 0,03, т.е. относительная частота заключена в границах от 0,07(0,1 – 0,03 = 0,07) до 0,13(0,1 + 0,03 = 0,13). Другими словами, число нестандартных деталей в 95,44% проб будет заключено между 28(7% от 400) и 52(13% от 400).

Если взять лишь одну пробу из 400 деталей, то с большой уверенностью можно ожидать, что в этой пробе будет нестандартных деталей ие менее 28 и не более 52. Возможно, хотя и маловероятно, что нестандартных деталей окажется меньше 28 либо больше 52.

Пример. Вероятность попадания в цель при одном выстреле равна 0,6. Найти вероятность того, что при n = 1200 независимых выстрелах отклонение «частости» от вероятности по модулю не превышает e = 0,03.

Решение.

.

Дата добавления: 2014-01-20