Закон распределения дискретной случайной величины. Многоугольник распределения

На первый взгляд может показаться, что для задания дискретной случайной величины достаточно перечислить все ее возможные значения. В действительности это не так: случайные величины могут иметь одинаковые перечни возможных значений, а вероятности их – различные. Поэтому для задания дискретной случайной величины недостаточно перечислить все возможные ее значения, нужно еще указать их вероятности.

Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически.

Определение. Любое правило (таблица, функция, график), позволяюшее находить вероятности произвольных событий A Í S (S – s-алгебра событий пространства W), в частности, указывающее вероятности отдельных значений случайной величины или множества этих значений, называется законом распределения случайной величины (или просто: распределением). Про с.в. говорят, что «она подчиняется данному закону распределения».

Пусть Х – д.с.в., которая принимает значения х ₁, х ₂, …, x_n,… (множество этих значений конечно или счетно) с некоторой вероятностью p_i, где i = 1,2,…, n,… Закон распределения д.с.в. удобно задавать с помощью формулы p_i = P { X = x_i }где i = 1,2,…, n,…, определяющей вероятность того, что в результате опыта с.в. Х примет значение x_i. Для д.с.в. Х закон распределения может быть задан в виде таблицы распределения:

Х	х 1	х 2	…	xn	…
P	р 1	р 2	…	рn	…

При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая – их вероятности. такую таблицу называют рядом распределения.

Приняв во внимание, что в одном испытании случайная величина принимает- одно и только одно возможное значение, заключаем, что события X = x ₁, X = x ₂,..., X = x_n образуют полную группу; следовательно, сумма вероятностей этих событий, т.е. сумма вероятностей второй строки таблицы, равна единице, то есть .

Если множество возможных значений X бесконечно (счетно), то ряд р ₁ + р ₂ +... сходится и его сумма равна единице.

Пример. В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 руб. и десять выигрышей по 1 руб. Найти закон распределения случайной величины X – стоимости возможного выигрыша для владельца одного лотерейного билета.

Решение. Напишем возможные значения X: х ₁ = 50, х ₂ = 1, х ₃ = 0. Вероятности этих возможных значений таковы: р ₁ = 0,01, р ₂ = 0,01, р ₃= 1 – (р ₁ + р ₂)=0,89.

Напишем искомый закон распределения:

Х
р	0,01	0,1	0,89

Контроль: 0,01 + 0,1 + 0,89 =1.

Пример. В урне 8 шаров, из которых 5 белых, остальные – черные. Из нее вынимают наудачу 3 шара. Найти закон распределения числа белых шаров в выборке.

Решение. Возможные значения с.в. Х – числа белых шаров в выборке есть х ₁ = 0, х ₂ = 1, х ₃ = 2, х ₄ = 3. Вероятности их соответственно будут

; ; .

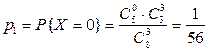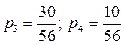Закон распределения запишем в виде таблицы.

Х
р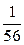

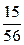
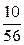
Контроль: .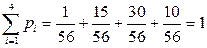

Закон распределения д.с.в. можно задать графически, если на оси абсцисс отложить возможные значения с.в., а на оси ординат – вероятности этих значений. ломаную, соединяющую последовательно точки (х ₁, р ₁), (х ₂, р ₂),… называют многоугольником (или полигоном) распределения (см. рис. 5.1).

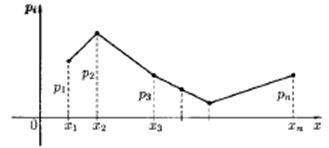
Рис. 5.1. Полигон распределения

Теперь можно дать более точное определение д.с.в.

Определение. Случайная величина Х дискретна, если существует конечное или счетное множество чисел х ₁, х ₂, … таких, что P { X = x_i } = p_i > 0 (i = 1,2,…) и p ₁ + p ₂ + р ₃ +… = 1.

Определим математические операции над дискретными с.в.

Определение. Суммой (разностью, произведением) д.с.в. Х, принимающей значения x_i с вероятностями p_i = P { X = x_i }, i = 1, 2, …, n, и д.с.в. Y, принимающей значения y_j с вероятностями p_j = P { Y = y_j }, j = 1, 2, …, m, называется д.с.в. Z = X + Y (Z = X – Y, Z = X×Y), принимающая значения z_ij = x_i + y_j (z_ij = x_i – y_j, z_ij = x_i×y_j) с вероятностями p_ij = P { X = x_i, Y = y_j } для всех указанных значений i и j. В случае совпадения некоторых сумм x_i + y_j (разностей x_i – y_j, произведений x_i×y_j)соответствующие вероятности складываются.

Определение. Произведение д.с.в. на число с называется д.с.в. сХ, принимающая значения сx_i с вероятностями p_i = P { X = x_i }.

Определение. Две д.с.в. Х и Y называются независимыми, если события { X = x_i } = A_i и { Y = y_j } = B_j независимы для любых i = 1, 2, …, n, j = 1, 2, …, m, то есть

.

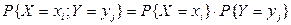В противном случае с.в. называют зависимыми. Несколько с.в. называют взаимно независимыми, если закон распределения любой из них не зависит от того, какие возможные значения приняли остальные величины.

Рассмотрим несколько наиболее часто употребляемых законов распределения.

Дата добавления: 2014-01-20