Начальные и центральные теоретические моменты

Рассмотрим дискретную случайную величину X, заданную законом распределения:

X
р	0,6	0,2	0,19	0,01

Найдем математическое ожидание X:

М (X) = 1×0,6 + 2×0,2 + 5×0,19+ 100× 0,01 =2,95.

Напишем закон распределения X ²:

X ^2
р	0,6	0,2	0,19	0,01

Найдем математическое ожидание X ²:

М (X ²) = 1×0,6 + 4×0,2 + 25×0,19 + 10000×0,01 = 106,15.

Видим, что М (X ²) значительно больше М (X). Это объясняется тем, что после возведения в квадрат возможное значение величины X ², соответствующее значению х = 100 величины X, стало равным 10 000, т.е. значительно увеличилось; вероятность же этого значения мала (0,01).

Таким образом, переход от М (X) к М (X ²) позволил лучше учесть влияние на математическое ожидание того возможного значения, которое велико и имеет малую вероятность. Разумеется, если бы величина X имела несколько больших и маловероятных значений, то переход к величине X ², а тем более к величинам X ³, X ⁴ и т.д., позволил бы еще больше «усилить роль» этих больших, но маловероятных возможных значений. Вот почему оказывается целесообразным рассматривать математическое ожидание целой положительной степени случайной величины (не только дискретной, но и непрерывной).

Определение. Начальным моментом порядка k случайной величины X называют математическое ожидание величины X^k:

v_k = M (X^k).

В частности,

v ₁ = M (X), v ₂ = M (X ²).

Пользуясь этими моментами, формулу для вычисления дисперсии D (X) = М (X ²) – [ М (X)]² можно записать так:

. (7.5)

Кроме моментов случайной величины X целесообразно рассматривать моменты отклонения X – М (X).

Определение. Центральным моментом порядка k случайной величины X называют математическое ожидание величины (X – М (X)) ^k:

.

В частности,

. (7.6)

. (7.7)

Легко выводятся соотношения, связывающие начальные и центральные моменты. Например, сравнивая (7.5) и (7.7), получим

.

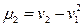Нетрудно, исходя из определения центрального момента и пользуясь свойствами математического ожидания, получить формулы:

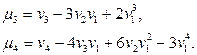
Моменты более высоких порядков применяются редко.

Замечание. Моменты, рассмотренные здесь, называют теоретическими. В отличие от теоретических моментов, моменты, которые вычисляются по данным наблюдений, называют эмпирическими.

Дата добавления: 2014-01-20