Свободные оси. Гироскопический эффект

Опыт показывает, что если тело привести во вращение вокруг некоторой оси, а затем предоставить его самому себе, то положение оси вращения в пространстве изменяется со временем. Сохранить неизменным положение оси вращения можно, если зафиксировать ее с помощью подшипников. Однако существуют такие оси вращения тел, которые не изменяют своей ориентации в пространстве без действия на них внешних сил. Эти оси называют свободными осями.

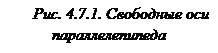В любом теле существуют три взаимно перпендикулярные оси, проходящие через центр масс тела, являющиеся осями симметрии, которые могут быть свободными осями.

Для устойчивости вращения большое значение имеет, какая именно из свободных осей служит осью вращения. Опыт показывает, что вращение вокруг осей с наибольшим и наименьшим моментами инерции оказывается устойчивым, а вращение вокруг оси со средним моментом инерции – неустойчивым.

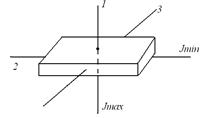
Так, если подбросить параллелепипед, приведя его одновременно во вращение, то он, падая, будет устойчиво вращаться вокруг осей 1 и 2 (рис. 4.7.1).

Свойство свободных осей сохранять свое положение в пространстве широко применяется в технике. Наиболее интересны в этом плане гироскопы – массивные однородные тела, вращающиеся с большой угловой скоростью вокруг своей оси симметрии, являющейся свободной осью.

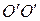Чтобы ось гироскопа изменила свое направление в пространстве, необходимо, чтобы момент внешних сил был отличен от нуля. При попытке вызвать поворот оси гироскопа наблюдается явление, получившее название гироскопического эффекта: под действием сил, которые должны были бы вызвать поворот оси гироскопа вокруг прямой , ось гироскопа поворачивается вокруг прямой (рис.4.7.2). Противоестественное на первый взгляд поведение гироскопа полностью соответствует законам динамики вращательного движения. Действительно, момент сил 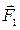и 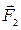, стремящихся повернуть ось гироскопа вокруг оси 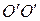, направлен вдоль прямой 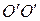влево (по правилу буравчика).

За время 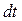момент импульса гироскопа получит приращение 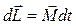, причем это приращение имеет такое же направление, как и 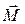(вектор 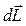лежит в плоскости чертежа и направлен влево). Спустя время 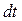момент импульса гироскопа станет равен 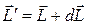(вектор 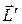лежит в плоскости рисунка). Так как направление момента импульса совпадает с направлением оси гироскопа, то направление 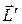совпадает с новым направлением оси гироскопа. Таким образом, ось гироскопа повернется на угол 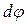вокруг оси .

Если ось гироскопа закреплена подшипниками, то вследствие гироскопического эффекта возникают гироскопические силы, действующие на опоры, в которых вращается ось гироскопа. Их необходимо учитывать при конструировании устройств, содержащих быстровращающиеся массивные составные части (например, подшипники паровых турбин на кораблях).

Гироскопы применяются в различных навигационных приборах (гирокомпас, гирогоризонт, авторулевой, автопилот и т.д.).

Глава 5. Механические колебания

Дата добавления: 2014-01-20