И вращательного движений

Основные динамические характеристики и законы поступательного

Поступательное движение	Вращательное движение
Основные динамические характеристики
мера инертности - масса		мера инертности - момент инерции
причина движения - сила		причина движения - момент силы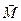
количество движения - импульс		количество движения - момент импульса
Основное уравнение динамики
Основные энергетические характеристики
работа	работа
мощность	мощность
кинетическая энергия	кинетическая энергия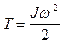

Пример 4.6.1. Платформа в виде диска радиусом и массой вращается по инерции около вертикальной оси с частотой . В центре платформы стоит человек массой . Какую линейную скорость относительно земли будет иметь человек, если перейдет на край платформы?

Решение:

Платформа с человеком составляет замкнутую механическую систему, поэтому момент импульса этой системы должен иметь постоянное значение. Следовательно, , где и 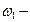момент инерции и угловая скорость системы, когда человек стоит в центре платформы; и момент инерции и угловая скорость системы, когда человек стоит на краю платформы.

Момент инерции системы равен сумме момента инерции человека (считаем его материальной точкой) и момента инерции платформы. Поэтому (момент инерции человека в первом случае равен 0) и .

Учитывая, что , запишем закон сохранения момента импульса:

, откуда .

Линейная скорость человека, стоящего на краю платформы, связана с угловой скоростью соотношением .

Таким образом,

Ответ: .

Пример 4.6.2. Маховик в виде диска массой и радиусом был раскручен до частоты и затем предоставлен самому себе. Вследствие трения маховик остановился. Найти момент сил трения, считая его постоянным, если маховик до полной остановки сделал 200 оборотов.

Решение:

Применим формулу, выражающую связь работы диссипативной силы с изменением кинетической энергии: .

Работа при вращательном движении определяется по формуле , где момент силы трения относительно оси вращения, угловое перемещение (угол поворота) маховика.

Изменение кинетической энергии вращающегося тела , где , а . Поскольку, сделав 200 оборотов, маховик остановился, то .

Следовательно, .

Таким образом, .

Знак «минус» показывает, что момент силы трения оказывает тормозящее действие.

Ответ: .

Пример 4.6.3. Карандаш длиной , поставленный вертикально, падает на стол. Какую угловую и линейную скорости будет иметь в момент соприкосновения со столом: 1) середина карандаша, 2) верхний его конец? Считать, что нижний конец карандаша не проскальзывает.

Решение:

При падении карандаш будет вращаться вокруг оси, проходящей через точку О (рис. 4.6.4). Внешние силы отсутствуют, поэтому система замкнута и выполняется закон сохранения полной механической энергии: Е₁=Е₂, где Е₁ – полная механическая энергия в первом состоянии системы (карандаш стоит вертикально); Е₂ – полная механическая энергия во втором состоянии – системы (карандаш касается стола после падения).

Полная механическая энергия в состоянии 1: , где (центр масс системы поднят на высоту, равную половине длины карандаша),(карандаш неподвижен).

Полная механическая энергия в состоянии 2:, где

(карандаш лежит на столе), . Момент инерции карандаша (стержня) относительно оси, проходящей через его край, находим по теореме Штейнера: . Поэтому .

Следовательно, любая точка карандаша (и середина, и верхний конец) вращается с угловой скоростью . Учитывая связь между линейной и угловой скоростью, находим, что линейная скорость середины карандаша (точка С) равна . Линейная скорость верхнего конца карандаша (точка А) равна .

Ответ: , , .

Дата добавления: 2014-01-20