
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Момент импульса. Закон сохранения момента импульса
|
|
|
|
Если сравнивать законы поступательного и вращательного движений, то усматривается аналогия между ними. Очевидно, что должен существовать и аналог импульса (количества движения) тела, называемый моментом импульса.
 Моментом импульса материальной точки относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:
Моментом импульса материальной точки относительно неподвижной точки О называется физическая величина, определяемая векторным произведением: 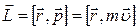 , где
, где  радиус–вектор, проведенный из центра вращения в данную материальную точку;
радиус–вектор, проведенный из центра вращения в данную материальную точку;  импульс материальной точки;
импульс материальной точки; 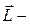 псевдовектор, его направление совпадает с направлением поступательного движения буравчика, рукоятка которого вращается от
псевдовектор, его направление совпадает с направлением поступательного движения буравчика, рукоятка которого вращается от 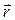 к
к 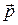 .
.
Численное значение момента импульса
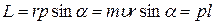 ,
,
где 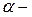 угол между векторами
угол между векторами 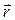 и
и 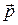 ,
, 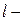 плечо вектора
плечо вектора  относительно точки О (рис. 4.6.1).
относительно точки О (рис. 4.6.1).
Моментом импульса относительно неподвижной оси Z называется скалярная величина, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси (рис. 4.6.2).
Необходимо отметить, что Lz не зависит от положения точки О на оси Z.
 Момент импульса системы материальных точек относительно оси есть сумма моментов импульсов материальных точек, входящих в систему, относительно этой оси:
Момент импульса системы материальных точек относительно оси есть сумма моментов импульсов материальных точек, входящих в систему, относительно этой оси:
 .
.
Пусть абсолютно твердое тело вращается вокруг неподвижной оси. Разобьем его на отдельные материальные точки массой 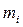 , которые движутся по окружности постоянного радиуса
, которые движутся по окружности постоянного радиуса 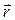 со скоростью
со скоростью  . Поскольку скорость
. Поскольку скорость  (и импульс
(и импульс  ) перпендикулярны этому радиусу, то радиус является плечом вектора импульса. Следовательно,
) перпендикулярны этому радиусу, то радиус является плечом вектора импульса. Следовательно,  .
.
Момент импульса тела как системы материальных точек:
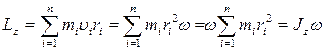 , где
, где 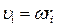 , а
, а  момент инерции тела относительно оси
момент инерции тела относительно оси 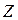 . Таким образом, момент импульса твердого тела относительно оси вращения равен произведению момента инерции тела относительно той же оси на угловую скорость.
. Таким образом, момент импульса твердого тела относительно оси вращения равен произведению момента инерции тела относительно той же оси на угловую скорость.
Запишем основное уравнение динамики вращательного движения через момент импульса. Для этого продифференцируем полученное уравнение по времени:
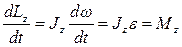 .
.
Следовательно, производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси: 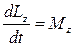 .
.
В векторной форме: 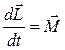 .
.
В замкнутой системе момент внешних сил 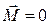 , следовательно
, следовательно  , поэтому
, поэтому
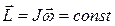 . (4.6.1)
. (4.6.1)

 Таким образом, момент импульса замкнутой системы сохраняется, т.е. не изменяется с течением времени. Это утверждение представляет собой закон сохранения момента импульса, который является фундаментальным законом природы.
Таким образом, момент импульса замкнутой системы сохраняется, т.е. не изменяется с течением времени. Это утверждение представляет собой закон сохранения момента импульса, который является фундаментальным законом природы.
Продемонстрировать выполнение закона сохранения момента импульса можно с помощью скамьи Жуковского – круглой платформы, которая без трения вращается вокруг вертикальной оси. Пусть человек стоит на скамье и держит в вытянутых руках гири (рис. 4.6.3, а). Платформа вместе с человеком вращается с угловой скоростью 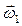 . Если человек прижмет гири к себе (рис. 4.6.3, б), то момент инерции системы уменьшится
. Если человек прижмет гири к себе (рис. 4.6.3, б), то момент инерции системы уменьшится  . Т.к. момент внешних сил равен нулю, выполняется закон сохранения момента импульса:
. Т.к. момент внешних сил равен нулю, выполняется закон сохранения момента импульса:  . Следовательно, угловая скорость вращения должна увеличиться
. Следовательно, угловая скорость вращения должна увеличиться  .
.
Сопоставим основные величины и уравнения, определяющие поступательное движение тела и его вращение вокруг неподвижной оси.
Таблица 4.6.1.
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 518; Нарушение авторских прав?; Мы поможем в написании вашей работы!