Основное уравнение динамики вращательного движения твердого тела

Работа при вращении тела идет на увеличение его кинетической энергии . Поскольку , то или .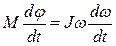

Учитывая, что , получим . Следовательно, момент силы,

действующей на тело, равен произведению момента инерции тела на угловое ускорение. Если ось вращения совпадает со свободной осью (см. 7.7), то имеет место векторное равенство

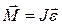. (4.5.1)

Это равенство представляет собой основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси.

Пример 4.5.1. Тонкий стержень длиной 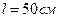и массой 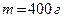вращается вокруг неподвижной оси с угловым ускорением . Ось вращения перпендикулярна стержню и проходит через его середину. Определить момент силы, действующий на стержень.

Решение:

Согласно основному уравнению динамики вращательного движения вращающий момент связан с угловым ускорением следующим соотношением: 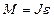; где 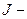момент инерции стержня относительно оси вращения. Т.к. ось вращения проходит через центр масс стержня, то .

Следовательно, момент силы, действующий на стержень, .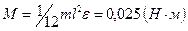

Ответ: .

Пример 4.5.2. Вал в виде сплошного цилиндра массой насажен на горизонтальную ось. На цилиндр намотан нерастяжимый шнур, к свободному концу которого подвешена гиря массой 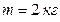. С каким ускорением будет опускаться гиря, если ее предоставить самой себе?

Решение:

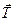Сделаем чертеж (рис. 4.5.1). Груз опускается с ускорением . На него действуют силы тяжести и натяжения шнура . Вал вращается против часовой стрелки с угловым ускорением 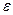. На вал действуют силы тяжести , сила реакции со стороны оси, на которую вал опирается, и сила реакции со стороны шнура . Вращающий момент создает только сила , т.к. линия действия сил 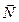и проходит через ось вращения (плечо этих сил равно 0).

Основное уравнение динамики поступательного движения груза имеет вид:

. В проекции на ось Oy: .

Основное уравнение динамики вращательного движения вала имеет вид: .

Если сила, действующая на тело, создает момент, способствующий вращению в заданном направлении, то ее момент считаем положительным (направление вектора момента силы 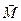совпадает с направлением углового ускорения ), если препятствует – момент считаем отрицательным (направления 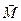и противоположны). Следовательно, в скалярной форме (в проекции на направление углового ускорения) основное уравнение динамики вращательного движения будет иметь вид: .

Учитывая, что ось вращения проходит через центр масс цилиндрического вала перпендикулярно плоскости его основания , где 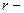радиус основания цилиндра, а вращающий момент (плечо силы равно радиусу основания цилиндра), то.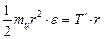

По третьему закону Ньютона 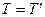(шнур нерастяжим), поэтому . Тангенциальное ускорение точек, лежащих на ободе вала, связано с его угловым ускорением соотношением: 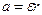. С таким же ускорением движется любая точка шнура, на котором подвешен груз. Следовательно, , откуда . Подставив в уравнение (1), получим:и .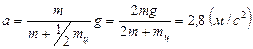

Ответ:.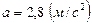

Пример 4.5.3. Через блок в виде диска, имеющего массу 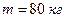, перекинута тонкая гибкая нить, к концам которой подвешены грузы массами и . С каким ускорением будут двигаться грузы, если их предоставить самим себе? Трением пренебречь.

Решение:

Сделаем чертеж (рис. 4.5.2). Первый груз будет двигаться поступательно вверх с ускорением , второй – опускаться с таким же ускорением. Уравнения поступательного движения грузов в векторной форме имеют вид .

В проекции на направление оси :

, откуда .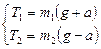

Согласно основному уравнению динамики вращательного движения . При движении грузов диск ускоренно вращается по часовой стрелке, следовательно, сила 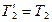способствует вращению 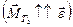, а сила 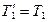тормозит вращение . Поэтому в скалярной форме (в проекции на направление углового ускорения)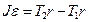, т.к. плечо сил равно радиусу диска .

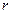Учитывая, что момент инерции диска 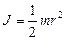, а линейное ускорение грузов равно

тангенциальному ускорению точек обода диска, связанного с угловым ускорением соот-

ношением 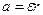, то , откуда .

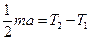Подставив в это выражение найденные ранее значения и , получим .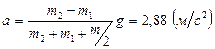

Ответ: .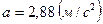

Пример 4.5.4. Вал массой и радиусом 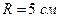вращался с частотой . К цилиндрической поверхности вала прижали тормозную колодку с силой , под действием которой вал остановился через 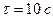. Определить коэффициент трения колодки о вал.

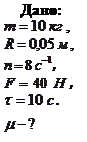
Решение:

Уравнение вращательного движения вала имеет вид: 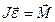. В скалярной форме (в проекции на направление углового ускорения) , где , 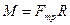. Сила трения, создающая тормозящий момент, связана с силой, прижимающей тормозную колодку к поверхности вала соотношением 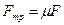. Угловая скорость вращения вала при равнозамедленном движении меняется со временем по закону 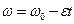, где 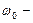начальная угловая скорость.

В момент остановки 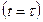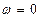, следовательно 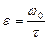. Учитывая связь угловой скорости с частотой вращения 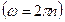, получим . Таким образом, , откуда .

Ответ: .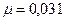

Дата добавления: 2014-01-20