Полные системы операций и функций. Алгебра Жегалкина

Преобразуем эту формулу, используя соответствующие эквивалентности. Из первой пары скобок вынесем P, из второй – Q.

U º .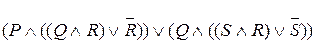

Воспользуемся эквиваленцией (по дистрибутивности)

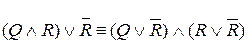º º .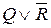

Аналогично для вторых скобок: .

Окончательно: U º .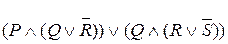

Изобразим схему, соответствующую заключительной формуле

Система операций å называется полной, если любая логическая операция может быть представлена формулой над å.

Так как всякая формула может быть представлена приведенной формулой, то система å₀ = {Ù, Ú, } – полна.

Система å сводится к å^*, обозначается å®å^*, если все операции системы å^* представимы формулами над системой å. Если å^* полна, то и å полна.

Последнее утверждение даёт один из способов доказательства полноты системы операций – сведение её к известной полной системе, например к å₀. То есть полной будет система å, через операции которой можно выразить конъюнкцию, дизъюнкцию и отрицание.

Так в силу законов де Моргана, полными будут и системы å₁ = {Ù, }, å₂ = {Ú, }, т.к. XÚY º Ø(ØX Ù ØY), а XÙY º Ø(ØX Ú ØY). Эти представления надо подставить в операции å₀ и получить å₂ и å₁, соответственно.

Алгебра над множеством высказываний с двумя операциями Ù и Å называется алгеброй Жегалкина. Напомним, что .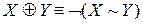

В алгебре Жегалкина выполняются следующие соотношения:

, ,

, ,

а также ассоциативность, коммутативность, идемпотентность конъюнкции и свойства констант.

Задание. Доказать полноту системы å = {Ù, Å}.

Решение. Сведем систему å к полной системе å₀.

.

Воспользуемся законом дистрибутивности для Ù и Å.

º

,

т.к (1Ù1)Å1º1Å1º0, а ХÅ0ºХ.

Если в произвольной формуле алгебры Жегалкина, реализующей булеву функцию f, раскрыть скобки и произвести все возможные упрощения, то получится формула, имеющая вид суммы произведений, то есть полинома по mod 2. Такая формула называется полиномом Жегалкина для данной функции. Линейной называется функция, полином Жегалкина которой линеен.

Задание. Представить формулу (x₁Ú x₂)Ù(Ú x₁Ùx₃) в виде полинома Жегалкина.

Решение. Воспользуемся полученным выше представлением дизъюнкции.

(x₁Ú x₂)Ù(Ú x₁Ùx₃) º (x₁Ùx₂ Å x₁ Å x₂) Ù (x₁Ù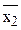Ùx₃ Å x₁Ùx₃ Å) º

º (x₁x₂ Å x₁ Å x₂)×(x₁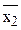x₃ Å x₁x₃ Å) º

º x₁x₂x₃ Å x₁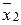x₃ Å x₁x₃ Å x₁Å x₁x₂x₃ º x₁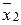x₃ Å x₁x₃ Åx₁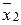º

º x₁ (x₂ Å 1) x₃ Å x₁ x₃ Å x₁ (x₂ Å 1) º x₁x₂x₃ Å x₁x₃ Å x₁x₃ Å x₁x₂ Å x₁ º

º x₁ x₂ x₃ Å x₁ x₂ Å x₁

В процессе преобразований мы несколько раз воспользовались тем, что ХÅХº0. Полученный полином не является линейным и имеет степень 3.

Сводимость к полной системе операций является необходимым условием полноты системы операций.

Теперь поговорим о полноте в терминах булевых функций.

Система булевых функций F называется полной, если любая функция может быть реализована формулой над F.

Замыканием множества F булевых функций (обозначается [F]) называется множество всех булевых функций, реализуемых формулами над F. Класс функций называется замкнутым, если [F] = F.

Примеры замкнутых классов.

1. Класс функций, сохраняющих 0.

.

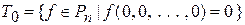2. Класс функций, сохраняющих 1.

.

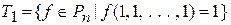3. Класс самодвойственных функций.

.

4. Класс монотонных функций.

, где

.

5. Класс линейных функций.

.

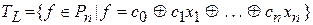Принадлежность некоторых функций этим классам оформим в виде таблицы.

Функция	Принадлежность классу
T 0	T 1	T ^*	T £	TL
	+ - - +	- + - +	- - + -	+ + - +	+ + + -

Из таблицы видно, что эти замкнутые классы попарно различны, не пусты и не совпадают с (множество всех булевых функций n переменных).

Теорема 7.1 (Поста). Система булевых функций полна тогда и только тогда, когда она содержит

- хотя бы одну функцию, не сохраняющую 0,

- хотя бы одну функцию, не сохраняющую 1,

- хотя бы одну несамодвойственную функцию,

- хотя бы одну немонотонную функцию и

- хотя бы одну нелинейную функцию.

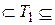Доказательство. Необходимость. Предположим противное, т.е. некоторая система булевых функций F полна ([F] =) и входит в один из упомянутых замкнутых классов (FÚ FÚ FÚ FÚ F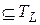). Обозначим через T_i тот класс, для которого справедливо включение F. Тогда [F] =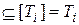, что противоречит тому, что ни один из классов не совпадает с .

Достаточность. Пусть система булевых функций F содержит хотя бы по одной функции, не принадлежащих каждому из замкнутых классов. Т.е.

$ F¢ = 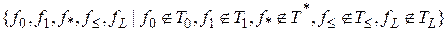Í F, причем функции не обязательно различны и не обязательно исчерпывают F. Покажем, что отрицание и конъюнкция, которые образуют полную систему булевых функций, реализуются формулами над F¢.

1) Проведем вначале построение вспомогательных формул над F¢. Реализуем константы 0 и 1, которые будут использоваться в формуле для конъюнкции.

Для реализации 1 воспользуемся функцией . Обозначим 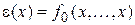. Так как , то . Если 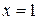, то возможны 2 случая:

a) и тогда реализует 1 (что нам и надо);

b) . В этом случае реализует отрицание. Для построения формулы, реализующей 1, воспользуемся функцией . Так как она несамосопряженная, то существует набор , на котором значение функции отличается от значения двойственной функции 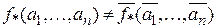. Тогда .

Рассмотрим функцию , для которой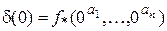

. Следовательно, является константой. Если 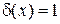, то она реализует 1, если , то реализацией 1 будет функция .

Константу 1 построили.

Константа 0 строится аналогично с использованием функции .

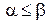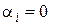2) Для построения формулы, реализующей функцию отрицания, воспользуемся немонотонной функцией . Так как , то , такие что . Зафиксируем их. Неравенство означает, что либо соответствующие координаты векторов и совпадают, либо и . Так как , то , а, следовательно, найдутся такие индексы, что . Обозначим через I множество таких индексов.

Определим функцию , где , если , и 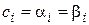, если . Вычислим значение функции 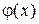в 0 и 1: , 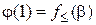. Так как , то , а это означает, что .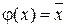

3) Для построения формулы, реализующей конъюнкцию, будем использовать нелинейную функцию 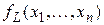. Так как , то её полином Жегалкина содержит слагаемое, являющееся конъюнкцией, по крайней мере, двух переменных.

Выберем произвольное нелинейное слагаемое, содержащее наименьшее число переменных. Пусть это . Рассмотрим функцию, полученную заменой всех переменных, не вошедших в это слагаемое, нулями, т.е. . Тогда все прочие нелинейные слагаемые обнулятся и останутся только выделенное слагаемое и линейные. Т.е. полином Жегалкина для имеет вид

.

Рассмотрим функцию (k > m ³1 – любое), где , , . Определим функцию

.

Такое представление корректно (в смысле представления конъюнкции над нашим базисом), так как являются константами 0 или 1, определенными ранее формулами над F¢, а сложение по модулю 2 с константой дает либо функцию, либо её отрицание, которое также выражено формулой над F¢(см. 2)).

Преобразуем , воспользовавшись представлением c.

. Таким образом, функция реализует конъюнкцию!!!!. Ч.т.д.

Дата добавления: 2014-01-20