Уравнение Ван-дер-Ваальса

В модели идеального газа не учитывались ни взаимодействия молекул, ни конечный размер самих молекул. Попытаемся учесть приближенно эти два обстоятельства. Для простоты рассмотрим 1 моль газа. Для него уравнение состояния идеального газа имеет вид:

. (3.9.1)

1. Учтем конечные собственные размеры молекул. Это приводит к тому, что объём, предоставленный молекулам газа для движения, будет меньше объёма сосуда V. Для этого заменим в уравнении (3.9.1) объём сосуда V на объём V – b, где b – характерная для данного газа положительная постоянная, учитывающая занимаемый молекулами объём.

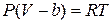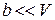, . (3.9.2)

2. Учтем проявляющееся на больших расстояниях притяжение между молекулами. Притяжение должно приводить к уменьшению давления газа на стенки сосуда, т.к. на каждую молекулу, находящуюся вблизи стенки сосуда, будет действовать со стороны других молекул сила, направленная внутрь сосуда. Поэтому уравнение (3.9.2) следует уточнить.

. (3.9.3)

Оценим поправку D P. На некоторую молекулу A, взаимодействующую со стенкой сосуда, действует сила со стороны остальных молекул, направленная внутрь сосуда. Эта сила, пропорциональна числу окружающих молекулу A молекул, т.е. пропорциональна плотности газа. Таким образом, поправка к передаваемому молекулой A импульсу при ударе о стенку пропорциональна плотности газа. Величина DP в формуле (3.9.3) будет пропорциональна переданному всеми молекулами импульсу, т.е. будет пропорциональна квадрату плотности газа, или обратно пропорциональна квадрату объёма:

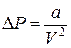, (3.9.4)

где a – характерная для данного газа положительная постоянная. При этом

.

В результате получим следующее уравнение состояния 1 моля газа:

. (уравнение Ван-дер-Ваальса) (3.9.5)

Исследуем зависимость P (V) при фиксированных значениях постоянных a и b для различных значений температуры T и построим графики этих зависимостей в координатах PV. Полученные кривые, называемые изотермами Ван-дер-Ваальса, приведены на рис. 3.9.1.

Как видно из этого рисунка для достаточно высокой температуры T ₁ изотерма Ван-дер-Ваальса мало отличается от изотермы идеального газа. При более низких температурах T ₂ и T ₃ изотермы содержат волнообразный участок. Существует некоторая температура T_к такая, что соответствующая ей изотерма отделяет все монотонные изотермы, лежащие выше нее, от «горбатых» изотерм, лежащих ниже. Такая температура T_к называется критической температурой, а соответствующая ей изотерма – критической изотермой.

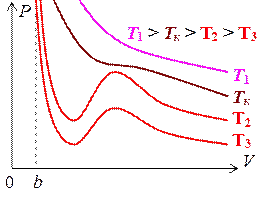
Рис. 3.9.1. Рис. 3.9.2.

Посмотрим, как уравнение Ван-дер-Ваальса описывает состояние реального газа. Для этого на одном рисунке изобразим изотерму Ван-дер-Ваальса и изотерму Эндрюса. Как видно из рисунка 3.9.2, изотерма Ван-дер-Ваальса (красная линия) и изотерма Эндрюса (синяя линия) практически совпадают при больших значениях V, соответствующих ненасыщенному пару. Качественно неплохо эти две кривые описывают жидкость. Вместе с тем изотерма Ван-дер-Ваальса не описывает область двухфазных состояний 14 (жидкость со своим насыщенным паром). Это объясняется неустойчивостью однородных состояний, отвечающих завитку 1-2-3-4. Рассмотрим эти неустойчивые состояния подробнее.

Процесс 2-3 неустойчив в принципе, т.к. в природе не существует веществ, для которых уменьшение объёма приводит к уменьшению давления, т.е. в этом случае наблюдается бесконечное сжатие вещества.

Процесс 1-2 отвечает состоянию перегретой жидкости. Такая жидкость при соблюдении специальных условий может существовать. В частности, если жидкость тщательно очистить от твердых примесей и растворенных в ней газов, то ее можно перевести в состояние с давлением, меньшим давления насыщенного пара, чтобы при этом жидкость не закипела. Такое состояние неустойчиво. Любая пылинка, попавшая в такую жидкость, приведет к ее бурному закипанию и переходу 2®2¢.

Процесс 3-4 отвечает состоянию пересыщенного пара. Такой пар, не содержащий посторонних включений, может находиться при давлении, большем давления насыщенного пара, т.е. при относительной влажности большей 100%. Это состояние неустойчиво и ведет к переходу 3®3¢ с конденсацией росы.

Выводы. Уравнение Ван-дер-Ваальса

1) хорошо описывает однофазные состояния (жидкость или ненасыщенный пар);

2) дает правильное представление о критическом состоянии вещества;

3) описывает такие экзотические состояния как перегретая жидкость или пересыщенный пар;

4) не описывает двухфазных состояний.

Дата добавления: 2014-01-20